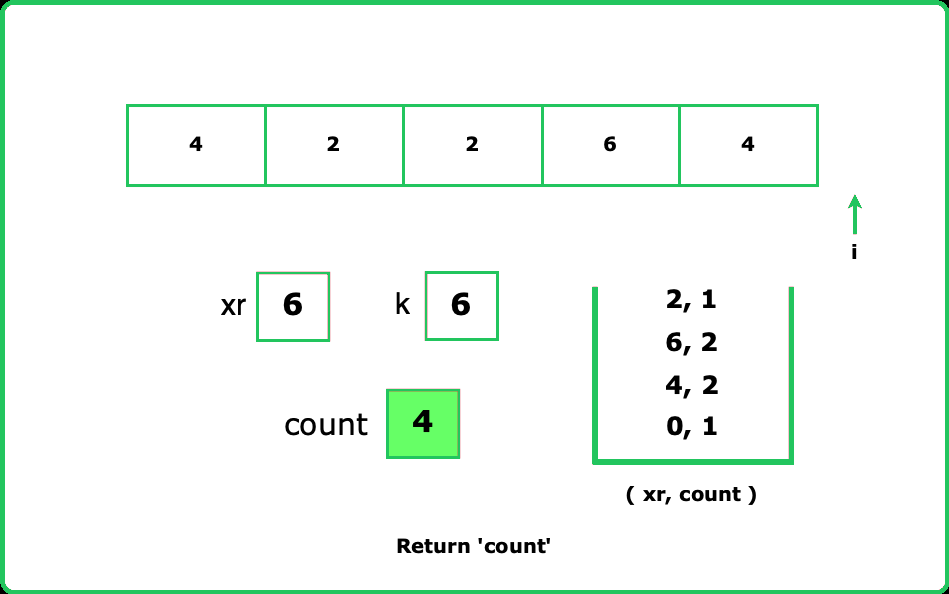
Count subarrays with given xor K
Hashing
FAQs
Hard
- Fun Fact: The underlying concept of this problem is extensively used in cryptographic algorithms and network protocols in the realm of Cybersecurity
- XOR operations, as used in this problem, are an integral part of many encryption methods for safeguarding data
- These are used not just for encoding messages, but also for error detections in data transmission and storage, as well as generating hash functions and pseudorandom number sequences
- A practical application of this problem's solution can hence lie in cracking certain encryption codes, or testing the strength of these encryption methodologies
Given an array of integers nums and an integer k, return the total number of subarrays whose XOR equals to k.
Examples:
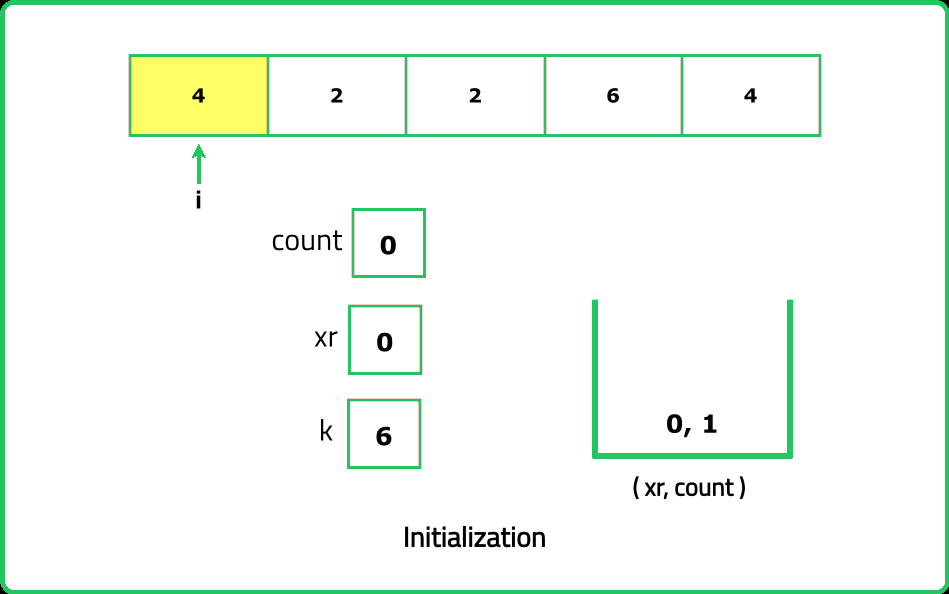
Input : nums = [4, 2, 2, 6, 4], k = 6
Output : 4
Explanation : The subarrays having XOR of their elements as 6 are [4, 2], [4, 2, 2, 6, 4], [2, 2, 6], and [6]
Input :nums = [5, 6, 7, 8, 9], k = 5
Output : 2
Explanation : The subarrays having XOR of their elements as 5 are [5] and [5, 6, 7, 8, 9]
Input : nums = [5, 2, 9], k = 7
Constraints
- 1 <= nums.length <= 105
- 1 <= nums[i] <= 109
- 1 <= k <= 109
Hints
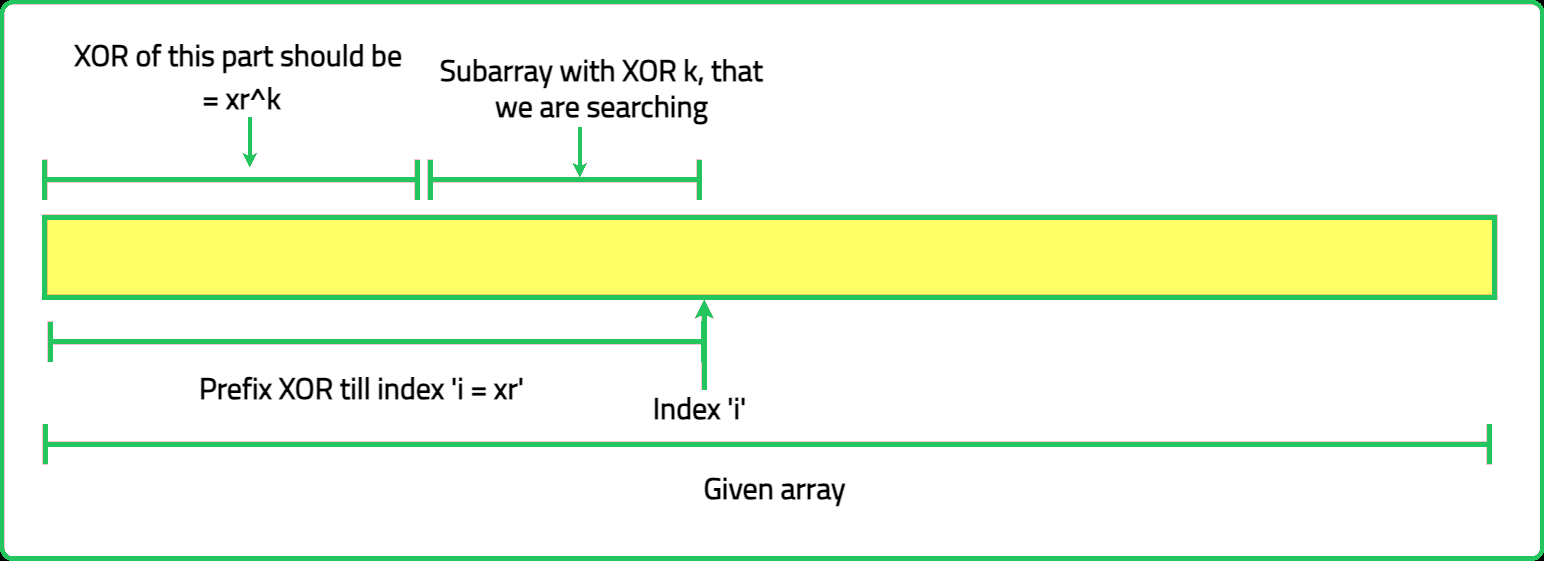
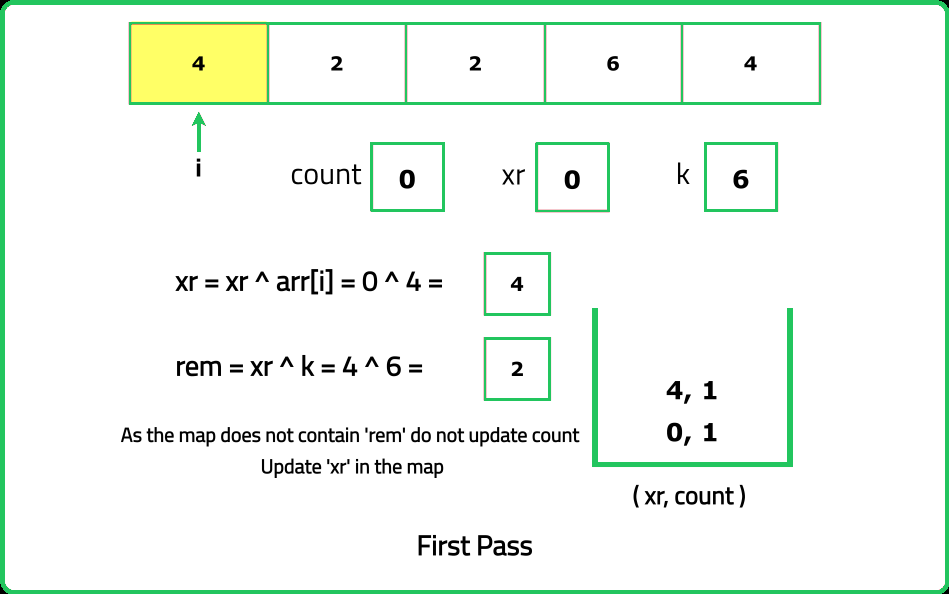
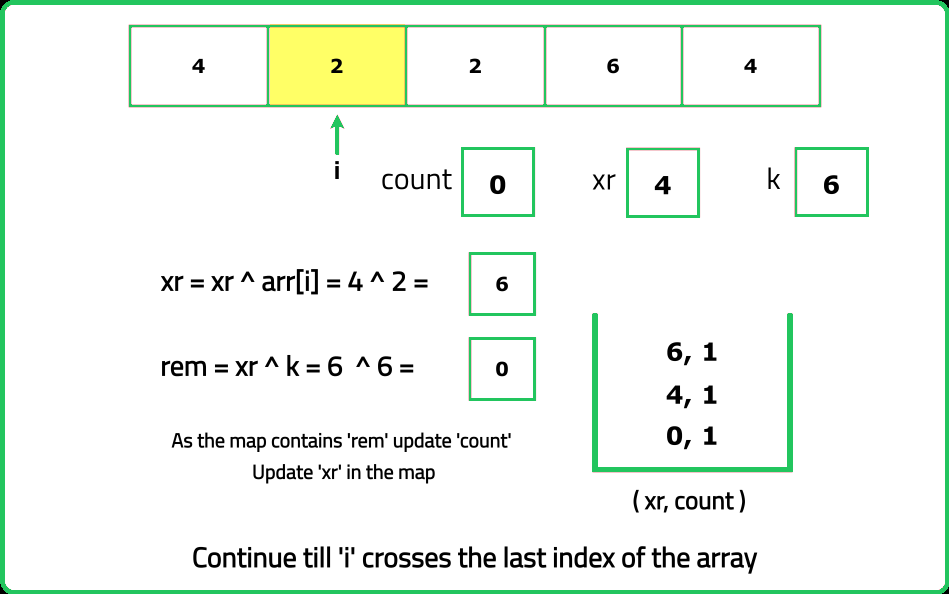
- Use a hash map to store the frequency of prefix XOR values encountered so far. This allows efficient computation of subarrays with a given XOR sum.
- For a subarray ending at index i, if prefixXOR[i]⊕k exists in the hash map, it means there is a subarray whose XOR is k. For each index, count the subarrays ending at that index that satisfy the XOR condition and update the hash map with the current prefix XOR.
Company Tags
Qualcomm
Seagate Technology
Twilio
PayPal
JPMorgan Chase
Instacart
Square
Etsy
Epic Games
Broadcom
Pinterest
Riot Games
Bungie
Reddit
Teladoc Health
Byju's
Siemens Healthineers
Roblox
Western Digital
OYO Rooms
Robinhood
Rockstar Games
Snowflake
Cerner
Databricks
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe