Merge Sorting
Sorting
Algorithms
Medium
- The merge sort algorithm, which is the core concept of this problem, is widely used in practical software development
- One fun fact is that it's the primary algorithm behind the efficient and powerful `sort()` function in many programming languages like Java and Python
- This method is used across a wide range of applications, from ranking search engine results to sorting a user's social media feed
- It's also often used in database algorithms for efficient data retrieval and storage
Given an array of integers, nums,sort the array in non-decreasing order using the merge sort algorithm. Return the sorted array.
A sorted array in non-decreasing order is one in which each element is either greater than or equal to all the elements to its left in the array.
Examples:
Input: nums = [7, 4, 1, 5, 3]
Output: [1, 3, 4, 5, 7]
Explanation: 1 <= 3 <= 4 <= 5 <= 7.
Thus the array is sorted in non-decreasing order.
Input: nums = [5, 4, 4, 1, 1]
Output: [1, 1, 4, 4, 5]
Explanation: 1 <= 1 <= 4 <= 4 <= 5.
Thus the array is sorted in non-decreasing order.
Input: nums = [3, 2, 3, 4, 5]
Constraints
- 1 <= nums.length <= 106
- -104 <= nums[i] <= 104
- nums[i] may contain duplicate values.
Hints
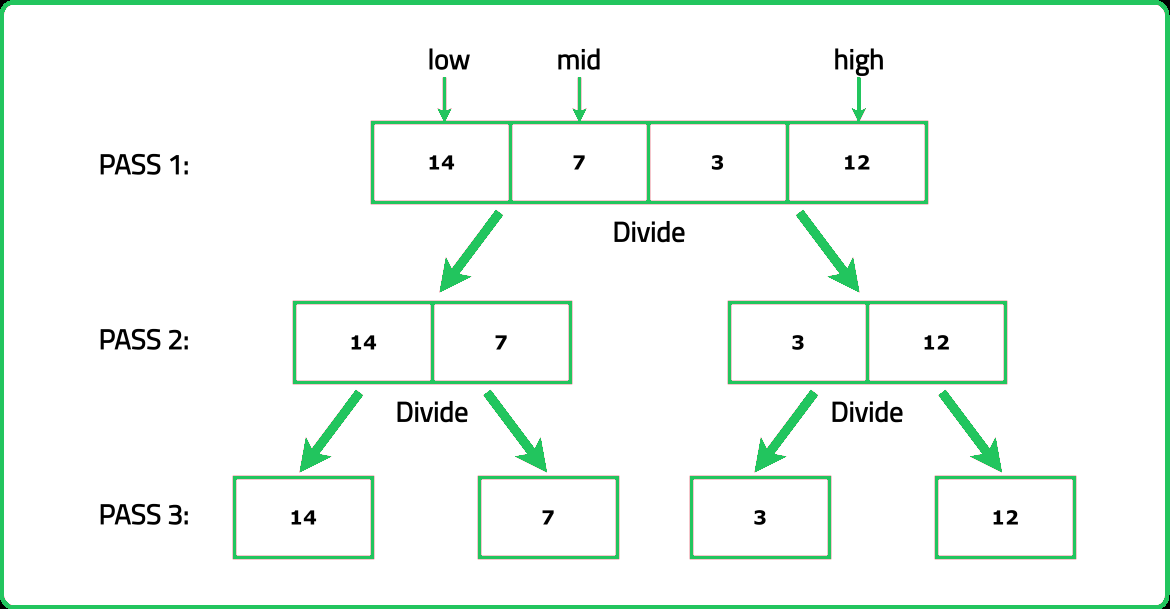
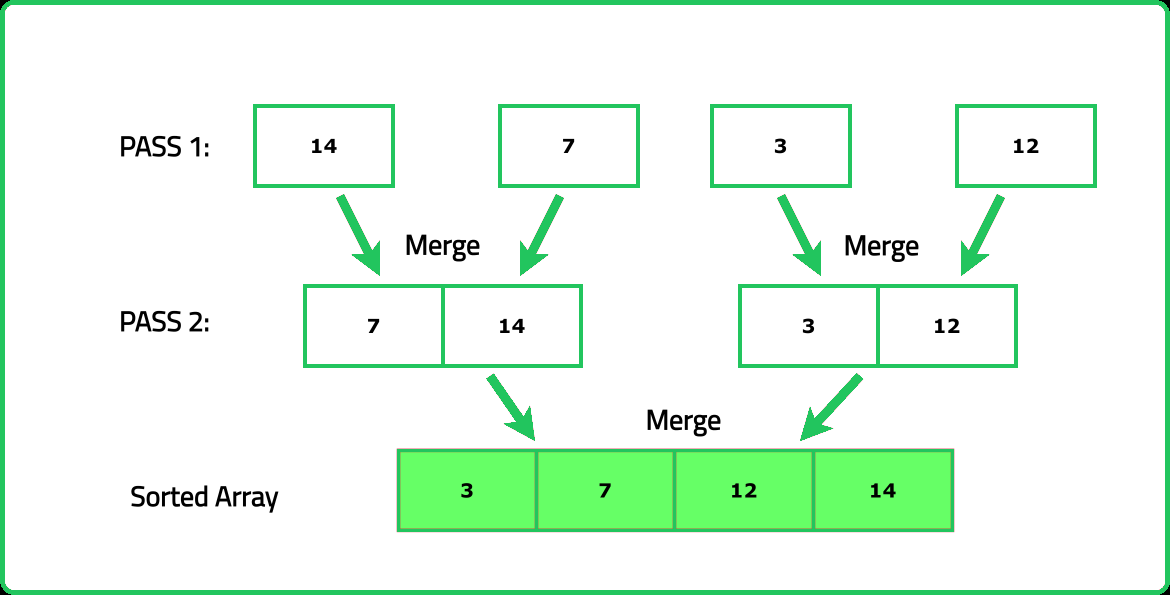
- Merge sort works by recursively dividing the array into two halves, sorting each half, and then merging the two sorted halves back together. Focus on understanding the "divide", "conquer", and "merge" steps.
- Think about how the recursive function handles sorting the left and right halves independently before merging them.
Company Tags
Mastercard
Stripe
Pinterest
ARM
Snowflake
Rockstar Games
Cerner
Splunk
Medtronic
Oracle
Broadcom
Uber
DoorDash
GE Healthcare
Nutanix
Electronic Arts
Docker
Epic Systems
Alibaba
HCL Technologies
Goldman Sachs
Red Hat
Seagate Technology
Optum
Airbnb
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro
Amazon
Google