Right/Left View of BT
Binary Trees
FAQs
Medium
- This programming problem is practically applied in database technologies that involve tree-based indexing like B-Trees or B+ Trees, commonly used in many SQL and NoSQL databases
- For instance, MongoDB utilizes a variant of B-tree data structure for its indexes
- Visibility from a certain perspective (here, it's from the right) can be used to optimize searches, traversals, or even distribution of nodes in parallel computing scenarios
- Hence, understanding these kinds of problems is key to designing efficient data management or networking systems
Assuming standing on the right side of a binary tree and given its root, return the values of the nodes visible, arranged from top to bottom.
Examples:
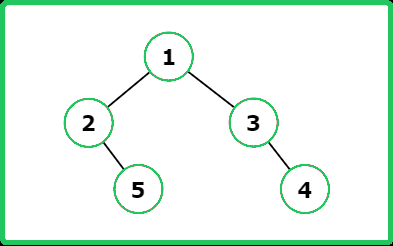
Input : root = [1, 2, 3, null, 5, null, 4]
Output : [1, 3, 4]
Explanation :
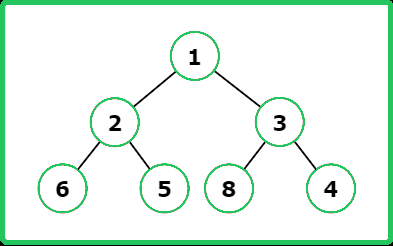
Input : root = [1, 2, 3, 6, 5, 8, 4]
Output : [1, 3, 4]
Explanation :
Input : root = [5, 1, 2, 8, null, 4, 5, null, 6]
Constraints
- 1 <= Number of Nodes <= 104
- -103 <= Node.val <= 103
Hints
- Use a queue to process nodes level by level, keeping track of their depth. At each level, store only the last node encountered in that level (i.e., the rightmost node). Process the right child first, then the left child, ensuring that the rightmost node is encountered first.
- Maintain a list (right_view[]) where right_view[level] stores the rightmost node at that level. The right_view list contains nodes arranged from top to bottom, forming the right-side view of the tree.
Company Tags
AMD
Micron Technology
Unity Technologies
Databricks
NVIDIA
Seagate Technology
Bloomberg
Deloitte
Alibaba
Goldman Sachs
Square
Bain & Company
IBM
Docker
Ernst & Young
Morgan Stanley
Snowflake
Pinterest
Johnson & Johnson
Stripe
Western Digital
Roche
OYO Rooms
DoorDash
Lyft
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition
The goal is to traverse a binary tree in a way that captures the nodes visible from the left and right perspectives. By utilizing a level-order traversal, each level of the tree is processed independently, ensuring that the structure and relationships between nodes are preserved. This traversal is facilitated using a queue to keep track of nodes at each level, allowing for a systematic exploration from the root to the deepest leaves. By maintaining a 2D array to record the nodes at each level, the left and right views can be easily extracted by focusing on the first and last nodes at each level, respectively.
Approach
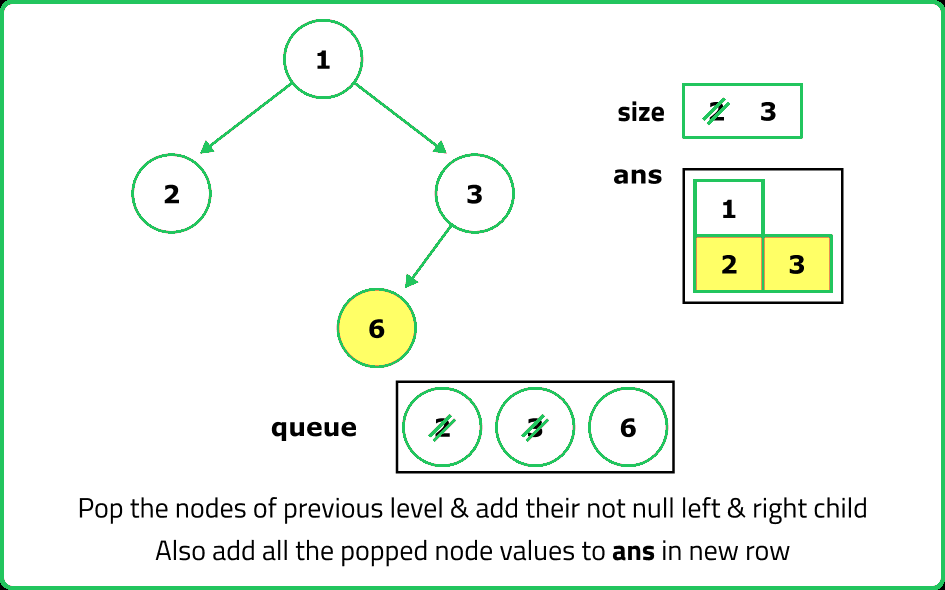
- Initialize an empty queue for storing nodes during traversal and a 2D array (or vector of vectors) for the level order traversal.
- If the tree is empty, return the empty 2D array and enqueue the root node into the queue.
- While the queue is not empty:
- Determine the current size of the queue, representing the number of nodes at the current level.
- Create a vector to store the nodes at the current level.
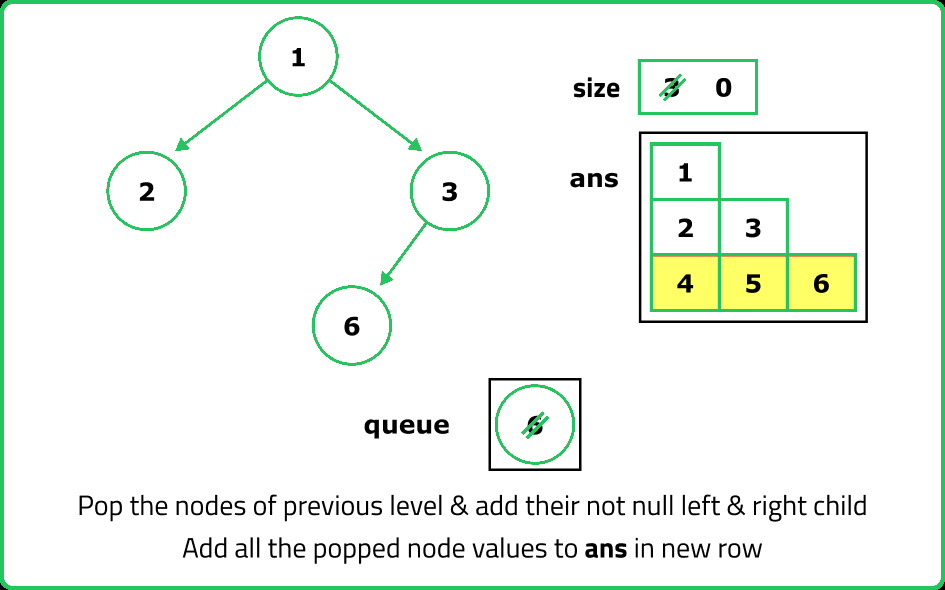
- For each node at the current level, dequeue the front node from the queue. Add the node’s value to the level vector. Enqueue the left and right children of the current node, if they exist.
- After processing all nodes at the current level, add the level vector to the 2D array.
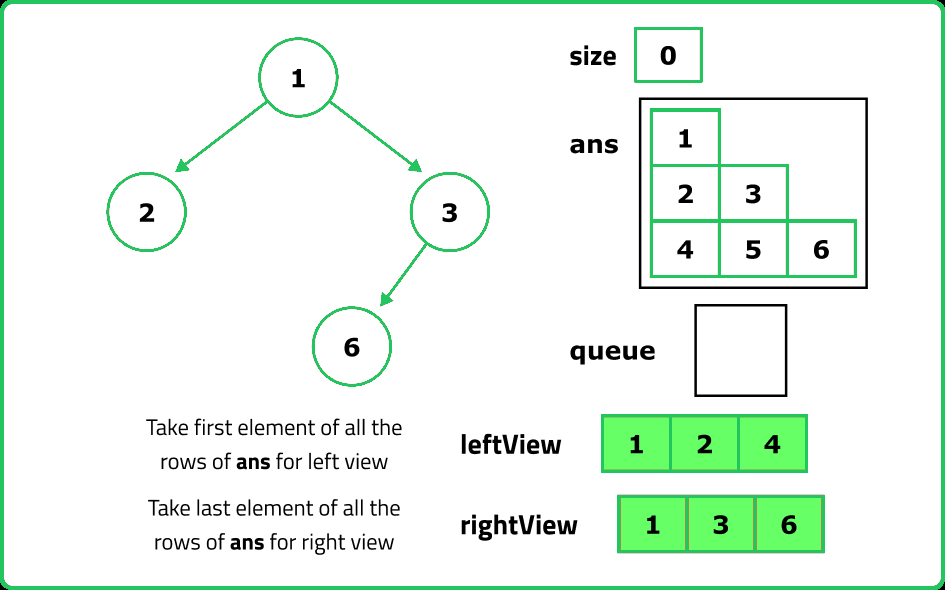
- To obtain the left view, extract the first element from each level's vector and store it in a separate array. This array represents the left view of the binary tree.
- To obtain the right view, extract the last element from each level's vector and store it in a separate array. This array represents the right view of the binary tree.
Dry Run
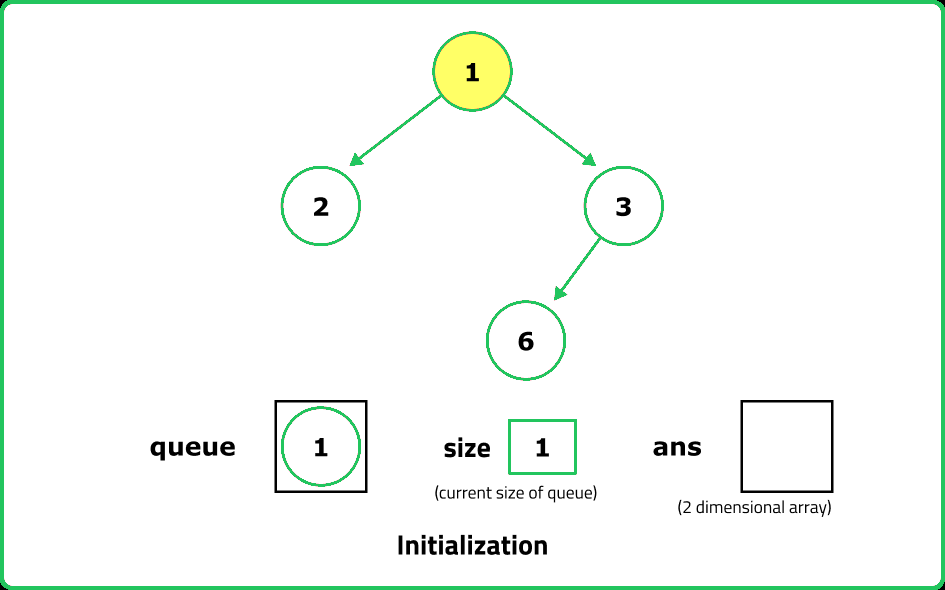
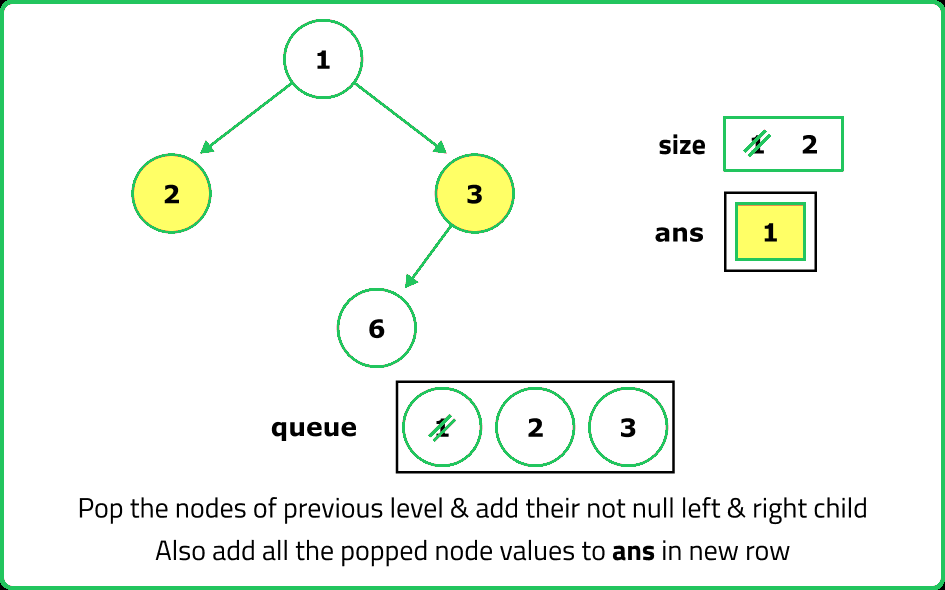
Solution
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124
#include <bits/stdc++.h>
using namespace std;
// Definition for a binary tree node.
struct TreeNode {
int data;
TreeNode *left;
TreeNode *right;
// Constructor to initialize the node with a value
TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution {
public:
// Function to return the Right view of the binary tree
vector<int> rightSideView(TreeNode* root) {
vector<int> res;
// Get the level order traversal of the tree
vector<vector<int>> levelTraversal = levelOrder(root);
// Iterate through each level and add the last element to the result
for (auto level : levelTraversal) {
res.push_back(level.back());
}
return res;
}
// Function to return the Left view of the binary tree
vector<int> leftSideView(TreeNode* root) {
vector<int> res;
// Get the level order traversal of the tree
vector<vector<int>> levelTraversal = levelOrder(root);
// Iterate through each level and add the first element to the result
for (auto level : levelTraversal) {
res.push_back(level.front());
}
return res;
}
private:
// Function that returns the level order traversal of a Binary tree
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
// Return an empty vector if the tree is empty
if (!root) {
return ans;
}
// Use a queue to perform level order traversal
queue<TreeNode*> q;
q.push(root);
while (!q.empty()) {
int size = q.size();
vector<int> level;
// Process each node in the current level
for (int i = 0; i < size; i++) {
TreeNode* top = q.front();
level.push_back(top->data);
q.pop();
// Enqueue the left child if it exists
if (top->left != NULL) {
q.push(top->left);
}
// Enqueue the right child if it exists
if (top->right != NULL) {
q.push(top->right);
}
}
// Add the current level to the result
ans.push_back(level);
}
return ans;
}
};
int main() {
// Creating a sample binary tree
TreeNode* root = new TreeNode(1);
root->left = new TreeNode(2);
root->left->left = new TreeNode(4);
root->left->right = new TreeNode(10);
root->left->left->right = new TreeNode(5);
root->left->left->right->right = new TreeNode(6);
root->right = new TreeNode(3);
root->right->right = new TreeNode(10);
root->right->left = new TreeNode(9);
Solution solution;
// Get the Right View traversal
vector<int> rightView = solution.rightSideView(root);
// Print the result for Right View
cout << "Right View Traversal: ";
for (auto node : rightView) {
cout << node << " ";
}
cout << endl;
// Get the Left View traversal
vector<int> leftView = solution.leftSideView(root);
// Print the result for Left View
cout << "Left View Traversal: ";
for (auto node : leftView) {
cout << node << " ";
}
cout << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122
import java.util.*;
class TreeNode {
int data;
TreeNode left;
TreeNode right;
// Constructor to initialize the node with a value
TreeNode(int val) {
data = val;
left = null;
right = null;
}
}
class Solution {
// Function to return the Right view of the binary tree
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
// Get the level order traversal of the tree
List<List<Integer>> levelTraversal = levelOrder(root);
// Iterate through each level and add the last element to the result
for (List<Integer> level : levelTraversal) {
res.add(level.get(level.size() - 1));
}
return res;
}
// Function to return the Left view of the binary tree
public List<Integer> leftSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
// Get the level order traversal of the tree
List<List<Integer>> levelTraversal = levelOrder(root);
// Iterate through each level and add the first element to the result
for (List<Integer> level : levelTraversal) {
res.add(level.get(0));
}
return res;
}
// Function that returns the level order traversal of a Binary tree
private List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ans = new ArrayList<>();
// Return an empty list if the tree is empty
if (root == null) {
return ans;
}
// Use a queue to perform level order traversal
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
while (!q.isEmpty()) {
int size = q.size();
List<Integer> level = new ArrayList<>();
// Process each node in the current level
for (int i = 0; i < size; i++) {
TreeNode top = q.poll();
level.add(top.data);
// Enqueue the left child if it exists
if (top.left != null) {
q.add(top.left);
}
// Enqueue the right child if it exists
if (top.right != null) {
q.add(top.right);
}
}
// Add the current level to the result
ans.add(level);
}
return ans;
}
public static void main(String[] args) {
// Creating a sample binary tree
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(10);
root.left.left.right = new TreeNode(5);
root.left.left.right.right = new TreeNode(6);
root.right = new TreeNode(3);
root.right.right = new TreeNode(10);
root.right.left = new TreeNode(9);
Solution solution = new Solution();
// Get the Right View traversal
List<Integer> rightView = solution.rightSideView(root);
// Print the result for Right View
System.out.print("Right View Traversal: ");
for (int node : rightView) {
System.out.print(node + " ");
}
System.out.println();
// Get the Left View traversal
List<Integer> leftView = solution.leftSideView(root);
// Print the result for Left View
System.out.print("Left View Traversal: ");
for (int node : leftView) {
System.out.print(node + " ");
}
System.out.println();
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102
from collections import deque
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.data = val
self.left = left
self.right = right
class Solution:
# Function to return the Right view of the binary tree
def rightSideView(self, root):
res = []
# Get the level order traversal of the tree
levelTraversal = self.levelOrder(root)
# Iterate through each level and add the last element to the result
for level in levelTraversal:
res.append(level[-1])
return res
# Function to return the Left view of the binary tree
def leftSideView(self, root):
res = []
# Get the level order traversal of the tree
levelTraversal = self.levelOrder(root)
# Iterate through each level and add the first element to the result
for level in levelTraversal:
res.append(level[0])
return res
# Function that returns the level order traversal of a Binary tree
def levelOrder(self, root):
ans = []
# Return an empty list if the tree is empty
if not root:
return ans
# Use a queue to perform level order traversal
q = deque([root])
while q:
size = len(q)
level = []
# Process each node in the current level
for i in range(size):
top = q.popleft()
level.append(top.data)
# Enqueue the left child if it exists
if top.left:
q.append(top.left)
# Enqueue the right child if it exists
if top.right:
q.append(top.right)
# Add the current level to the result
ans.append(level)
return ans
# Main method to test the functionality
if __name__ == "__main__":
# Creating a sample binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.left.left = TreeNode(4)
root.left.right = TreeNode(10)
root.left.left.right = TreeNode(5)
root.left.left.right.right = TreeNode(6)
root.right = TreeNode(3)
root.right.right = TreeNode(10)
root.right.left = TreeNode(9)
solution = Solution()
# Get the Right View traversal
rightView = solution.rightSideView(root)
# Print the result for Right View
print("Right View Traversal:", end=" ")
for node in rightView:
print(node, end=" ")
print()
# Get the Left View traversal
leftView = solution.leftSideView(root)
# Print the result for Left View
print("Left View Traversal:", end=" ")
for node in leftView:
print(node, end=" ")
print()
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109
// Definition for a binary tree node.
class TreeNode {
constructor(val = 0, left = null, right = null) {
this.data = val;
this.left = left;
this.right = right;
}
}
class Solution {
// Function to return the Right view of the binary tree
rightSideView(root) {
let res = [];
// Get the level order traversal of the tree
let levelTraversal = this.levelOrder(root);
// Iterate through each level and add the last element to the result
for (let level of levelTraversal) {
res.push(level[level.length - 1]);
}
return res;
}
// Function to return the Left view of the binary tree
leftSideView(root) {
let res = [];
// Get the level order traversal of the tree
let levelTraversal = this.levelOrder(root);
// Iterate through each level and add the first element to the result
for (let level of levelTraversal) {
res.push(level[0]);
}
return res;
}
// Function that returns the level order traversal of a Binary tree
levelOrder(root) {
let ans = [];
// Return an empty array if the tree is empty
if (!root) {
return ans;
}
// Use a queue to perform level order traversal
let q = [];
q.push(root);
while (q.length > 0) {
let size = q.length;
let level = [];
// Process each node in the current level
for (let i = 0; i < size; i++) {
let top = q.shift();
level.push(top.data);
// Enqueue the left child if it exists
if (top.left !== null) {
q.push(top.left);
}
// Enqueue the right child if it exists
if (top.right !== null) {
q.push(top.right);
}
}
// Add the current level to the result
ans.push(level);
}
return ans;
}
}
// Main function to test the functionality
(function main() {
// Creating a sample binary tree
let root = new TreeNode(1);
root.left = new TreeNode(2);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(10);
root.left.left.right = new TreeNode(5);
root.left.left.right.right = new TreeNode(6);
root.right = new TreeNode(3);
root.right.right = new TreeNode(10);
root.right.left = new TreeNode(9);
let solution = new Solution();
// Get the Right View traversal
let rightView = solution.rightSideView(root);
// Print the result for Right View
console.log("Right View Traversal:", rightView.join(" "));
// Get the Left View traversal
let leftView = solution.leftSideView(root);
// Print the result for Left View
console.log("Left View Traversal:", leftView.join(" "));
})();
Complexity Analysis
Time Complexity: O(N): Each node in the binary tree is processed exactly once, either enqueued or dequeued, resulting in a linear time complexity relative to the number of nodes, N.
Space Complexity: O(N): The space complexity is determined by the maximum number of nodes stored in the queue at any point during the traversal. In the worst case, this could be all nodes of the last level of the binary tree, which could amount to N/2 nodes.
Intuition
To obtain the left and right views of a binary tree, a depth-first traversal is employed. This approach tracks the level of each node, ensuring that only the first node encountered at each level is included in the result. For both views, the traversal starts from the root and progresses through each level, capturing the required nodes based on the traversal order. The left view prioritizes left children first, while the right view prioritizes right children first.
Approach
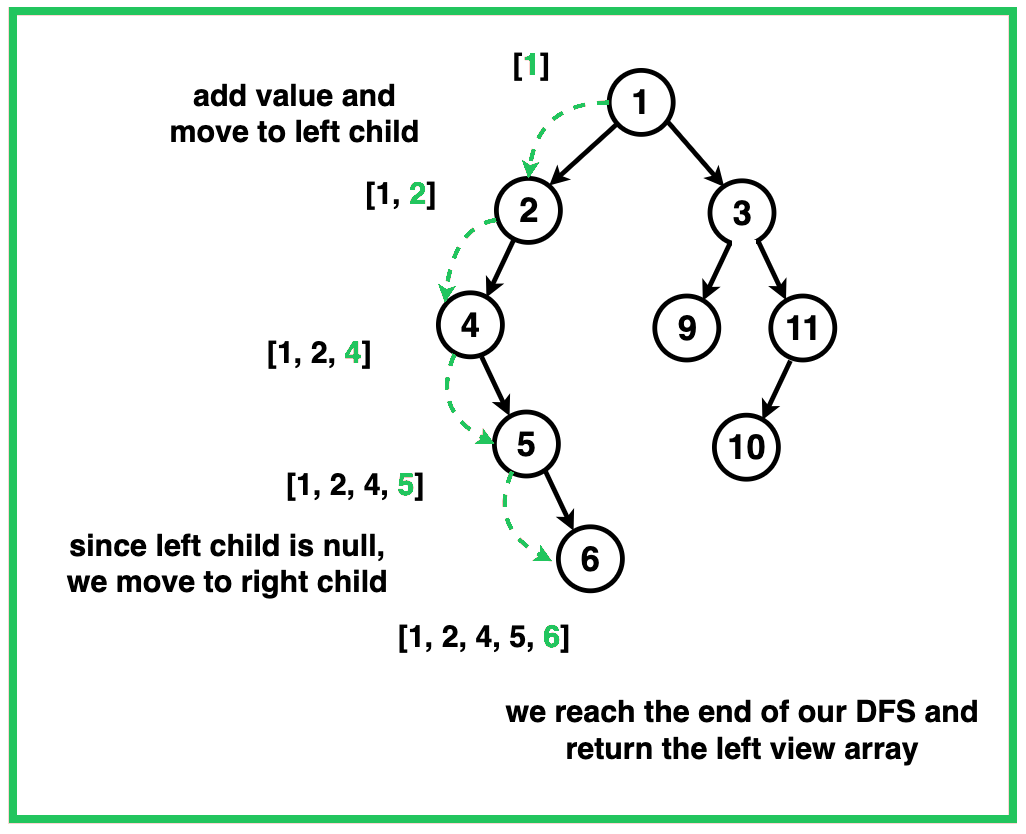
Algorithm for Left View
- Begin by initializing an empty vector named
resto hold the nodes visible from the left view of the binary tree. - Implement a recursive depth-first search (DFS) approach to traverse the tree:
- Base Case: If the current node is
null, terminate the recursion as this indicates the end of a vertical level. - Recursive Function: Define the function to accept the current node, its vertical level, and the result vector
resas parameters. - Within the recursive function, check if the size of
resis equal to the current level. If true, add the value of the current node tores, as this is the first node encountered at this vertical level. - Proceed by making a recursive call to the function for the left child of the current node, followed by the right child, incrementing the level by 1 for each call. This ensures nodes are processed from top to bottom, left to right.
- Base Case: If the current node is
- Continue the recursion process until all nodes are traversed and the base case is encountered. Return the vector
res, which will now contain the nodes visible from the left view of the tree.
Algorithm for Right View
- Start by initializing an empty vector named
resto store the nodes visible from the right view of the binary tree. - Implement a recursive depth-first search (DFS) approach for traversal:
- Base Case: If the current node is
null, return from the recursion, indicating the end of the current vertical level. - Recursive Function: The function should accept the current node, its vertical level, and the result vector
resas arguments. - Within the recursive function, check if the size of
resmatches the current level. If so, add the current node's value tores, as this node is the first encountered at this vertical level from the right side. - Make a recursive call for the right child of the current node first, followed by the left child, incrementing the level by 1 for each recursive call. This ensures that nodes on the right side are prioritized, providing the right view.
- Base Case: If the current node is
- Continue the recursive process until all nodes have been visited and the base case is reached. Finally, return the vector
res, which now includes the nodes visible from the right view of the binary tree.
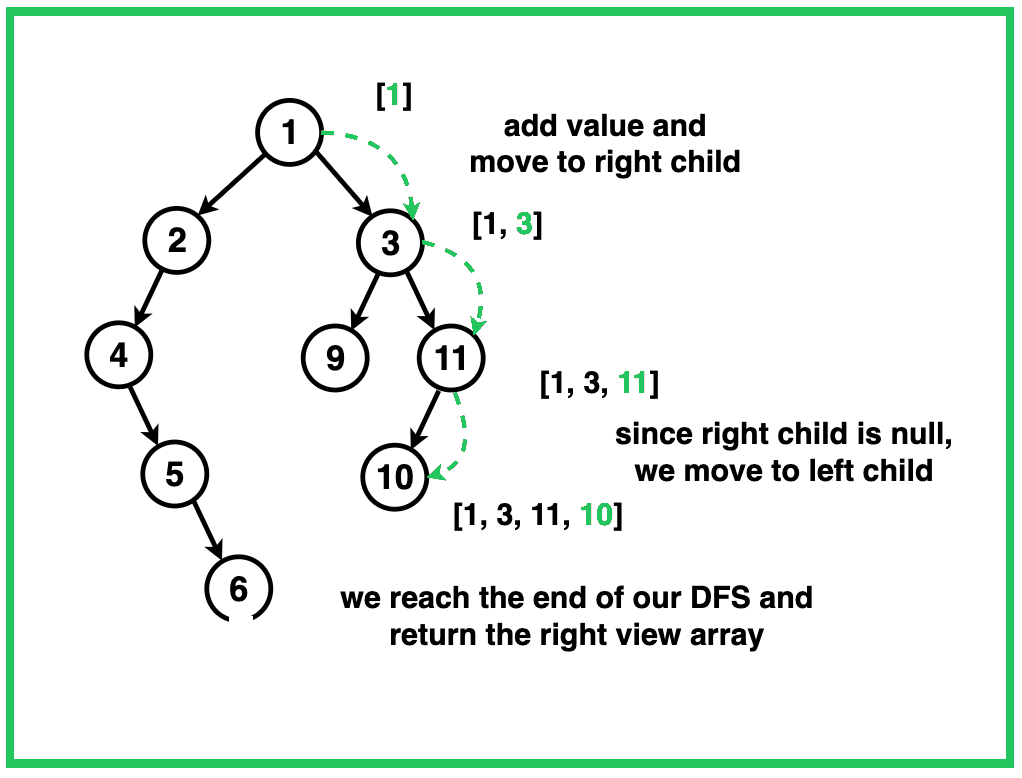
Solution
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899
#include <bits/stdc++.h>
using namespace std;
// Node structure for the binary tree
struct Node {
int data;
Node* left;
Node* right;
// Constructor to initialize the node with a value
Node(int val) : data(val), left(nullptr), right(nullptr) {}
};
class Solution {
public:
// Function to return the Right view of the binary tree
vector<int> rightsideView(Node* root) {
vector<int> res;
// Call the recursive function to populate the right-side view
recursionRight(root, 0, res);
return res;
}
// Function to return the Left view of the binary tree
vector<int> leftsideView(Node* root) {
vector<int> res;
// Call the recursive function to populate the left-side view
recursionLeft(root, 0, res);
return res;
}
private:
// Recursive function to traverse the binary tree and populate the left-side view
void recursionLeft(Node* root, int level, vector<int>& res) {
if (root == nullptr) {
return;
}
if (res.size() == level) {
res.push_back(root->data);
}
recursionLeft(root->left, level + 1, res);
recursionLeft(root->right, level + 1, res);
}
// Recursive function to traverse the binary tree and populate the right-side view
void recursionRight(Node* root, int level, vector<int>& res) {
if (root == nullptr) {
return;
}
if (res.size() == level) {
res.push_back(root->data);
}
recursionRight(root->right, level + 1, res);
recursionRight(root->left, level + 1, res);
}
};
int main() {
// Creating a sample binary tree
Node* root = new Node(1);
root->left = new Node(2);
root->left->left = new Node(4);
root->left->right = new Node(10);
root->left->left->right = new Node(5);
root->left->left->right->right = new Node(6);
root->right = new Node(3);
root->right->right = new Node(10);
root->right->left = new Node(9);
Solution solution;
// Get the Right View traversal
vector<int> rightView = solution.rightsideView(root);
// Print the result for Right View
cout << "Right View Traversal: ";
for (auto node : rightView) {
cout << node << " ";
}
cout << endl;
// Get the Left View traversal
vector<int> leftView = solution.leftsideView(root);
// Print the result for Left View
cout << "Left View Traversal: ";
for (auto node : leftView) {
cout << node << " ";
}
cout << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112
import java.util.*;
class TreeNode {
int data;
TreeNode left;
TreeNode right;
// Constructor to initialize the node with a value
TreeNode(int val) {
data = val;
left = null;
right = null;
}
}
class Solution {
// Function to return the Right view of the binary tree
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
// Call the recursive function to populate the right-side view
recursionRight(root, 0, res);
return res;
}
// Function to return the Left view of the binary tree
public List<Integer> leftSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
// Call the recursive function to populate the left-side view
recursionLeft(root, 0, res);
return res;
}
// Recursive function to traverse the binary tree and populate the left-side view
private void recursionLeft(TreeNode root, int level, List<Integer> res) {
// Check if the current node is NULL
if (root == null) {
return;
}
// Check if the size of the result list is equal to the current level
if (res.size() == level) {
// If equal, add the value of the current node to the result list
res.add(root.data);
}
// Recursively call the function for the left child with an increased level
recursionLeft(root.left, level + 1, res);
// Recursively call the function for the right child with an increased level
recursionLeft(root.right, level + 1, res);
}
// Recursive function to traverse the binary tree and populate the right-side view
private void recursionRight(TreeNode root, int level, List<Integer> res) {
// Check if the current node is NULL
if (root == null) {
return;
}
// Check if the size of the result list is equal to the current level
if (res.size() == level) {
// If equal, add the value of the current node to the result list
res.add(root.data);
}
// Recursively call the function for the right child with an increased level
recursionRight(root.right, level + 1, res);
// Recursively call the function for the left child with an increased level
recursionRight(root.left, level + 1, res);
}
public static void main(String[] args) {
// Creating a sample binary tree
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(10);
root.left.left.right = new TreeNode(5);
root.left.left.right.right = new TreeNode(6);
root.right = new TreeNode(3);
root.right.right = new TreeNode(10);
root.right.left = new TreeNode(9);
Solution solution = new Solution();
// Get the Right View traversal
List<Integer> rightView = solution.rightSideView(root);
// Print the result for Right View
System.out.print("Right View Traversal: ");
for (int node : rightView) {
System.out.print(node + " ");
}
System.out.println();
// Get the Left View traversal
List<Integer> leftView = solution.leftSideView(root);
// Print the result for Left View
System.out.print("Left View Traversal: ");
for (int node : leftView) {
System.out.print(node + " ");
}
System.out.println();
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.data = val
self.left = left
self.right = right
class Solution:
# Function to return the Right view of the binary tree
def rightSideView(self, root):
res = []
# Call the recursive function to populate the right-side view
self.recursionRight(root, 0, res)
return res
# Function to return the Left view of the binary tree
def leftSideView(self, root):
res = []
# Call the recursive function to populate the left-side view
self.recursionLeft(root, 0, res)
return res
# Recursive function to traverse the binary tree and populate the left-side view
def recursionLeft(self, root, level, res):
# Check if the current node is NULL
if root is None:
return
# Check if the size of the result list is equal to the current level
if len(res) == level:
# If equal, add the value of the current node to the result list
res.append(root.data)
# Recursively call the function for the left child with an increased level
self.recursionLeft(root.left, level + 1, res)
# Recursively call the function for the right child with an increased level
self.recursionLeft(root.right, level + 1, res)
# Recursive function to traverse the binary tree and populate the right-side view
def recursionRight(self, root, level, res):
# Check if the current node is NULL
if root is None:
return
# Check if the size of the result list is equal to the current level
if len(res) == level:
# If equal, add the value of the current node to the result list
res.append(root.data)
# Recursively call the function for the right child with an increased level
self.recursionRight(root.right, level + 1, res)
# Recursively call the function for the left child with an increased level
self.recursionRight(root.left, level + 1, res)
# Main method to test the functionality
if __name__ == "__main__":
# Creating a sample binary tree
root = TreeNode(1)
root.left = TreeNode(2)
root.left.left = TreeNode(4)
root.left.right = TreeNode(10)
root.left.left.right = TreeNode(5)
root.left.left.right.right = TreeNode(6)
root.right = TreeNode(3)
root.right.right = TreeNode(10)
root.right.left = TreeNode(9)
solution = Solution()
# Get the Right View traversal
rightView = solution.rightSideView(root)
# Print the result for Right View
print("Right View Traversal:", end=" ")
for node in rightView:
print(node, end=" ")
print()
# Get the Left View traversal
leftView = solution.leftSideView(root)
# Print the result for Left View
print("Left View Traversal:", end=" ")
for node in leftView:
print(node, end=" ")
print()
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899
// Definition for a binary tree node.
class TreeNode {
constructor(val = 0, left = null, right = null) {
this.data = val;
this.left = left;
this.right = right;
}
}
class Solution {
// Function to return the Right view of the binary tree
rightSideView(root) {
let res = [];
// Call the recursive function to populate the right-side view
this.recursionRight(root, 0, res);
return res;
}
// Function to return the Left view of the binary tree
leftSideView(root) {
let res = [];
// Call the recursive function to populate the left-side view
this.recursionLeft(root, 0, res);
return res;
}
// Recursive function to traverse the binary tree and populate the left-side view
recursionLeft(root, level, res) {
// Check if the current node is NULL
if (root === null) {
return;
}
// Check if the size of the result list is equal to the current level
if (res.length === level) {
// If equal, add the value of the current node to the result list
res.push(root.data);
}
// Recursively call the function for the left child with an increased level
this.recursionLeft(root.left, level + 1, res);
// Recursively call the function for the right child with an increased level
this.recursionLeft(root.right, level + 1, res);
}
// Recursive function to traverse the binary tree and populate the right-side view
recursionRight(root, level, res) {
// Check if the current node is NULL
if (root === null) {
return;
}
// Check if the size of the result list is equal to the current level
if (res.length === level) {
// If equal, add the value of the current node to the result list
res.push(root.data);
}
// Recursively call the function for the right child with an increased level
this.recursionRight(root.right, level + 1, res);
// Recursively call the function for the left child with an increased level
this.recursionRight(root.left, level + 1, res);
}
}
// Main method to test the functionality
(() => {
// Creating a sample binary tree
const root = new TreeNode(1);
root.left = new TreeNode(2);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(10);
root.left.left.right = new TreeNode(5);
root.left.left.right.right = new TreeNode(6);
root.right = new TreeNode(3);
root.right.right = new TreeNode(10);
root.right.left = new TreeNode(9);
const solution = new Solution();
// Get the Right View traversal
const rightView = solution.rightSideView(root);
// Print the result for Right View
console.log("Right View Traversal:", rightView.join(" "));
// Get the Left View traversal
const leftView = solution.leftSideView(root);
// Print the result for Left View
console.log("Left View Traversal:", leftView.join(" "));
})();
Complexity Analysis
Time Complexity: O(N), where N is the number of nodes in the tree.
As each node is visited once and for each node, we perform a constant amount of work (checking conditions and making at most two recursive calls). Thus, the time complexity is O(N).
Space Complexity: O(H), where H is the height of the binary tree.
Because of the recursive stack space which depends on the height of the tree.
Note:
- In a balanced tree, height H is nearly equal to logN. Hence, the best-case space complexity is O(logN).
- In a skewed tree, height H is almost equal to N. Hence, the worst-case space complexity turns out to be O(N).
Frequently Occurring Doubts
Q: How do we ensure the rightmost node is stored at each level?
A: By processing the right child first, we ensure that the first node encountered at a level is the rightmost one.
Q: Can this problem be solved using a recursive DFS approach?
A: Yes! In a recursive approach, we: Use preorder traversal (Root → Right → Left). Maintain a depth variable and track the first node encountered at each depth. If a node is the first node encountered at its depth, it is added to the result.
Interview Followup Questions
Q: How would you modify the approach to return the left-side view instead?
A: Instead of processing the right child first, process the left child first.
Q: Can we solve this problem using a single list instead of a queue?
A: The queue is needed to maintain level-order traversal, so while a single list wouldn't store all nodes, we could optimize memory by modifying it in place.
Notes
Code
✅ Testcase
Input: {'root': '1 2 3 null 5 null 4'}
Expected:
1 3 4
1 3 4
Actual: -
Time: -
sec
Status: Waiting
Input: {'root': '1 2 3 6 5 8 4'}
Expected:
1 3 4
1 3 4
Actual: -
Time: -
sec
Status: Waiting
Input: {'root': '1 2 3 4 5 null 6 7 8'}
Expected:
1 3 6 8
1 3 6 8
Actual: -
Time: -
sec
Status: Waiting