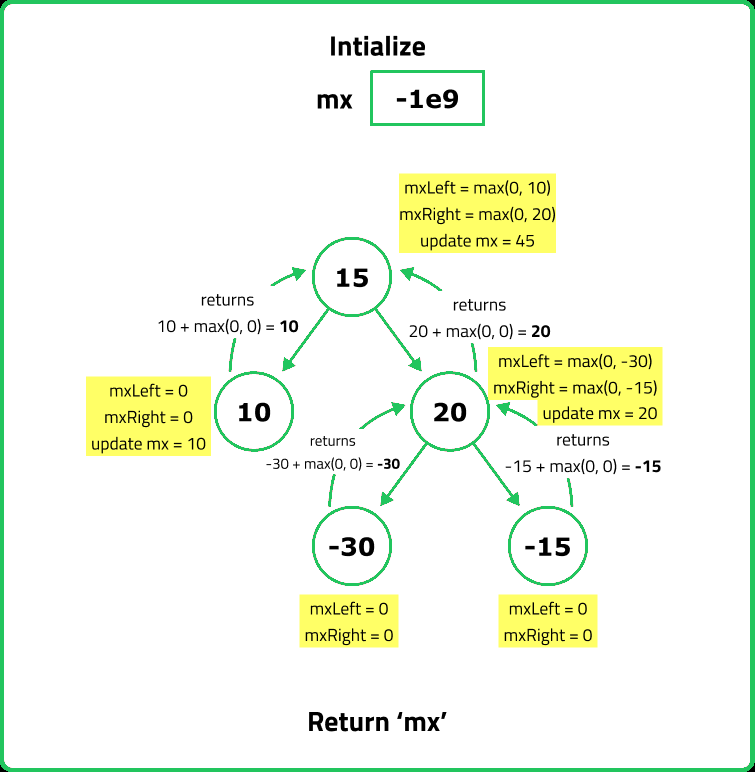
Maximum path sum
Binary Trees
Medium Problems
Medium
- Fun Fact: The concept used in this problem is fundamental in the development of networking or routing protocols in the field of computer networks
- Specifically, in routing tables, each path could be seen as a route and each node as a network point
- The path sum could represent the total cost or delay of the route
- By determining the path with the "largest" or "smallest" sum, network devices can decide the best path for data transmission
- Similarly, file systems in Operating Systems use the same concept where they need to find the best path (with maximum or minimum resource usage) to store or retrieve data
- It's an underlying concept also used in database indexing and many algorithms in artificial intelligence and machine learning
In a binary tree, a path is a list of nodes where there is an edge between every pair of neighbouring nodes. A node may only make a single appearance in the sequence. The total of each node's values along a path is its path sum. Return the largest path sum of all non-empty paths given the root of a binary tree.
Note: The path does not have to go via the root.
Examples:
Input : root = [20, 9, -10, null, null, 15, 7]
Output : 34
Explanation : The path from node 15 to node 9 has maximum path sum.
The path is 15 -> -10 -> 20 -> 9.
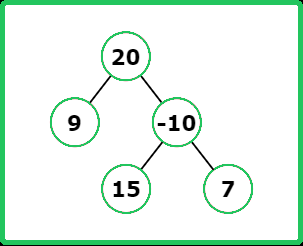
Input : root = [-10, 9, 20, null, null, 15, 7]
Output : 42
Explanation : The path from node 15 to node 7 has maximum path sum.
The path is 15 -> 20 -> 7.
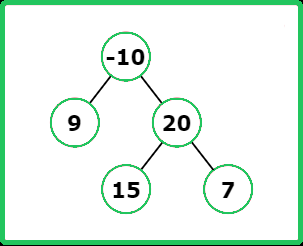
Input : root = [1, 2, 3, null, 4]
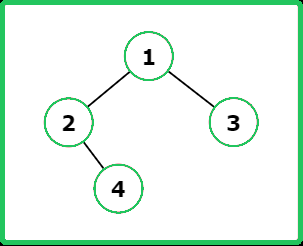
Constraints
- 1 <= Number of Nodes <= 3*104
- -103 <= Node.val <= 103
Hints
- Compute the maximum path sum ending at the current node as the max of:max(left subtree sum,right subtree sum)+current node value. (This ensures we include only one child when extending the path upwards).
- Compute the maximum sum passing through the node by considering both children and the node’s value:left sum+right sum+node value. Maintain a global maximum that tracks the highest encountered path sum.
Company Tags
Alibaba
Bain & Company
Databricks
Goldman Sachs
Activision Blizzard
Morgan Stanley
Medtronic
Dropbox
ARM
Seagate Technology
Walmart
Cloudflare
Zoho
Boston Consulting Group
PwC
Reddit
Cerner
HCL Technologies
Western Digital
Siemens Healthineers
Snowflake
Splunk
Byju's
Rakuten
Roblox
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe