Minimum path sum in grid

Why Greedy Approach will not work:

As the question asks for minimum path sum, the first approach that comes to our mind is to take a greedy approach and always form a path by locally choosing the cheaper option. At every cell, we have three choices, to move to the bottom cell, move to the bottom-left cell or move to the bottom-right cell. Our ultimate aim is to provide a path that provides us the least path sum. Therefore at every cell, we will make the choice to move which costs us less.

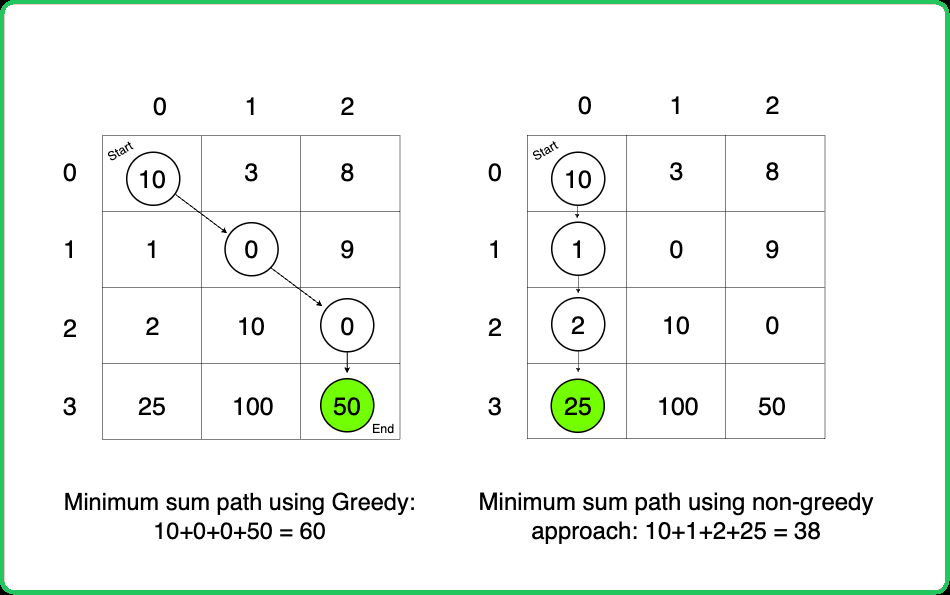
We can clearly see the issue with the greedy solution. When we make local choices, we might select a path that ends up costing us much more later on.

Therefore, the only alternative left to us is to generate all possible paths and determine which path has the minimum path sum. To generate all paths, we will use recursion.

Steps to form the recursive solution:

Express the problem in terms of indexes: We are given a matrix with the number of rows equal to N and number of column as M. We can define the function with two parameters i and j, where i and j represent the row and column of the matrix.

Now, our ultimate aim is to reach the last row. We can define f(i,j) such that it gives us the minimum path sum from the first row to the cell [i][j].

Try out all possible choices at a given index: At every index there are three choices, one to go to the bottom cell, next to go bottom-left cell and other to the bottom-right cell. To go to the bottom increase i by 1, to go to bottom-left increase i by and decrease j by 1, to move towards the bottom-right, increase both i and j by 1.

Now when we get our answer for the recursive call (f(i+1,j), f(i+1, j-1) or f(i+1,j+1)), the current cell value also needs to be added to it as we have to include it too for the current path sum

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j){
    //Base case
     down =  mat[i][j] + f(i+1, j)
    diagonalRight = mat[i][j] + f(i+1, j+1)
    diagonalLeft = mat[i][j] + f(i+1, j-1)
}

Take the minimum of all choices: As question asks to find the minimum path sum of all the possible unique paths, return the minimum of the choices(down, diagonalLeft, diagonalRight)

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j){
    //Base case
    down =  mat[i][j] + f(i+1, j)
    diagonalRight = mat[i][j] + f(i+1, j+1)
    diagonalLeft = mat[i][j] + f(i+1, j-1)
    return min(down, diagonalLeft, diagonalRight)
}

Base cases: When i == 0, it means we are at the first row, so the min path from that cell to the firstrow will be the value of that cell itself, hence we return mat[0][j].

At every cell there are three options, move to the top cell (↑), to the top-right cell(↗), or to the top-left cell(↖). As we are writing recursion in top-down manner (from the last row to the first row).

As we are moving to the top cell (↑), at max we will reach the first row, from where we return, so we will never go out of the bound index. To move to the top-left cell(↖) or to the top-right cell(↗), it can happen that we may go out of bound as shown in the figure(below). So we need to handle it, return INT_MAX, whenever we go out of bound, in this way this path will not be selected by the calling function as we are returning the minimum path.

/*It is pseudocode  and it is not tied to 
any specific programming  language*/

f(i,j){
    if(j < 0 || j > M)   return   INT_MAX
    if(i == 0)   return mat[0][j]
    //code
}

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to recursively find the 
    minimum path sum for a given cell*/
    int func(int i, int j, int m, vector<vector<int>> &matrix) {
        // Base Conditions
        if (j < 0 || j >= m)
            return 1e9; 
        if (i == 0)
            return matrix[0][j]; 
    
        /* Calculate the minimum path sum by 
        considering three possible directions:
        up, left diagonal, and right diagonal*/
        int up = matrix[i][j] + func(i - 1, j, m, matrix);
        int leftDiagonal = matrix[i][j] + func(i - 1, j - 1, m, matrix);
        int rightDiagonal = matrix[i][j] + func(i - 1, j + 1, m, matrix);
    
        // Return the minimum of the three paths 
        return min(up, min(leftDiagonal, rightDiagonal));
}
public:
    /* Function to find the minimum
    path sum in the given matrix*/
    int minFallingPathSum(vector<vector<int>> &matrix) {
        int n = matrix.size(); 
        int m = matrix[0].size(); 
    
        int mini = INT_MAX; 
    
        /* Iterate through each cell in the first row 
        to find minimum path sum starting from each of them*/
        for (int j = 0; j < m; j++) {
            int ans = func(n - 1, j, m, matrix); 
            mini = min(mini, ans); 
        }
        // Return the minimum path sum
        return mini; 
    }
};

int main() {
    vector<vector<int>> matrix{{1, 2, 10, 4}, {100, 3, 2, 1}, {1, 1, 20, 2}, {1, 2, 2, 1}};
    
    //Create an instance of Solution class
    Solution sol;
    
    // Call the getMinPathSum function and print the result
    cout << sol.minFallingPathSum(matrix) << endl;

    return 0;
}
import java.util.*;

class Solution {
    /* Function to recursively find the
    minimum path sum for a given cell*/
    private int func(int i, int j, int m, int[][] matrix) {
        // Base Conditions
        if (j < 0 || j >= m)
            return (int) 1e9; 
        if (i == 0)
            return matrix[0][j]; 
    
        /* Calculate the minimum path sum by 
        considering three possible directions:
        up, left diagonal, and right diagonal*/
        int up = matrix[i][j] + func(i - 1, j, m, matrix);
        int leftDiagonal = matrix[i][j] + func(i - 1, j - 1, m, matrix);
        int rightDiagonal = matrix[i][j] + func(i - 1, j + 1, m, matrix);
    
        // Return the minimum of the three paths 
        return Math.min(up, Math.min(leftDiagonal, rightDiagonal));
    }

    // Function to find the minimum path sum in given matrix
    public int minFallingPathSum(int[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
    
        int mini = Integer.MAX_VALUE;
    
        /* Iterate through each cell in the first row to 
        find minimum path sum starting from each of them*/
        for (int j = 0; j < m; j++) {
            int ans = func(n - 1, j, m, matrix);
            mini = Math.min(mini, ans);
        }
        // Return the minimum path sum
        return mini;
    }

    public static void main(String[] args) {
        int[][] matrix = {
            {1, 2, 10, 4},
            {100, 3, 2, 1},
            {1, 1, 20, 2},
            {1, 2, 2, 1}
        };
    
        // Create an instance of Solution class
        Solution sol = new Solution();
    
        // Call the minFallingPathSum function and print the result
        System.out.println(sol.minFallingPathSum(matrix));
    }
}
class Solution:
    """ Function to recursively find the 
    minimum path sum for a given cell"""
    def func(self, i, j, m, matrix):
        # Base Conditions
        if j < 0 or j >= m:
            return int(1e9)
        if i == 0:
            return matrix[0][j]
    
        """ Calculate the minimum path sum by 
        considering three possible directions:
            up, left diagonal, and right diagonal"""
        up = matrix[i][j] + self.func(i - 1, j, m, matrix)
        left_diagonal = matrix[i][j] + self.func(i - 1, j - 1, m, matrix)
        right_diagonal = matrix[i][j] + self.func(i - 1, j + 1, m, matrix)
    
        # Return the minimum of the three paths
        return min(up, min(left_diagonal, right_diagonal))
    
    # Function to find the minimum path sum in given matrix
    def minFallingPathSum(self, matrix):
        n = len(matrix)
        m = len(matrix[0])
    
        mini = float('inf')
    
        """ Iterate through each cell in the first row to
        find minimum path sum starting from each of them"""
        for j in range(m):
            ans = self.func(n - 1, j, m, matrix)
            mini = min(mini, ans)
        
        # Return the minimum path sum
        return mini

if __name__ == "__main__":
    matrix = [
        [1, 2, 10, 4],
        [100, 3, 2, 1],
        [1, 1, 20, 2],
        [1, 2, 2, 1]
    ]
    
    # Create an instance of Solution class
    sol = Solution()
    
    # Call the minFallingPathSum function and print the result
    print(sol.minFallingPathSum(matrix))
class Solution {
    /* Function to recursively find the
    minimum path sum for a given cell*/
    func(i, j, m, matrix) {
        // Base Conditions
        if (j < 0 || j >= m)
            return 1e9;
        if (i === 0)
            return matrix[0][j];
    
        /* Calculate the minimum path sum by 
        considering three possible directions:
        up, left diagonal, and right diagonal*/
        const up = matrix[i][j] + this.func(i - 1, j, m, matrix);
        const leftDiagonal = matrix[i][j] + this.func(i - 1, j - 1, m, matrix);
        const rightDiagonal = matrix[i][j] + this.func(i - 1, j + 1, m, matrix);
    
        // Return the minimum of the three paths
        let temp = Math.min(leftDiagonal, rightDiagonal);
        return Math.min(up, temp);
    }
    
    // Function to find the minimum path sum in given matrix
    minFallingPathSum(matrix) {
        const n = matrix.length;
        const m = matrix[0].length;
    
        let mini = Infinity;
    
        /* Iterate through each cell in the first row to
        find minimum path sum starting from each of them*/
        for (let j = 0; j < m; j++) {
            const ans = this.func(n - 1, j, m, matrix);
            mini = Math.min(mini, ans);
        }
        
        // Return the minimum path sum
        return mini;
    }
}

const matrix = [
    [1, 2, 10, 4],
    [100, 3, 2, 1],
    [1, 1, 20, 2],
    [1, 2, 2, 1]
];

// Create an instance of Solution class
const sol = new Solution();

// Call the minFallingPathSum function and print the result
console.log(sol.minFallingPathSum(matrix));

Complexity Analysis:

Time Complexity: O(2^N), where N is the number of rows . As, each cell has 2 choices and at max the number of subproblems can be N.

Space Complexity:O(N), The depth of the recursion is proportional to the height of the triangle N. Therefore, the space used by the call stack is O(N).

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence the DP approaches can be applied to the recursive solution.

In order to convert a recursive solution to memoization the following steps will be taken:

The dp array stores the calculations of subproblems, dp[i][j] represents the minimum path sum to reach (0,0) from (i,j). Initially, fill the array with -1, to indicate that no subproblem has been solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.

Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution{
private:
    /* Function to recursively find the 
    minimum path sum for a given cell*/
    int func(int i, int j, int m, vector<vector<int>> &matrix, vector<vector<int>> &dp) {
        // Base Conditions
        if (j < 0 || j >= m)
            return 1e9; 
        if (i == 0)
            return matrix[0][j]; 
        
        /* If the result for this cell is
        already calculated, return it*/
        if (dp[i][j] != -1)
            return dp[i][j];
    
        /* Calculate the minimum path sum by 
        considering three possible directions:
        up, left diagonal, and right diagonal*/
        int up = matrix[i][j] + func(i - 1, j, m, matrix, dp);
        int leftDiagonal = matrix[i][j] + func(i - 1, j - 1, m, matrix, dp);
        int rightDiagonal = matrix[i][j] + func(i - 1, j + 1, m, matrix, dp);
    
        // Store the minimum of the three paths in dp
        return dp[i][j] = min(up, min(leftDiagonal, rightDiagonal));
}
public:
    /* Function to find the minimum
    path sum in the given matrix*/
    int minFallingPathSum(vector<vector<int>> &matrix) {
        int n = matrix.size(); 
        int m = matrix[0].size(); 
    
        // Memoization table to store computed results
        vector<vector<int>> dp(n, vector<int>(m, -1)); 
    
        int mini = INT_MAX; 
    
        /* Iterate through each cell in the first row 
        to find minimum path sum starting from each of them*/
        for (int j = 0; j < m; j++) {
            int ans = func(n - 1, j, m, matrix, dp); 
            mini = min(mini, ans); 
        }
        // Return the minimum path sum
        return mini; 
    }
};

int main() {
    vector<vector<int>> matrix{{1, 2, 10, 4}, {100, 3, 2, 1}, {1, 1, 20, 2}, {1, 2, 2, 1}};
    
    //Create an instance of Solution class
    Solution sol;
    
    // Call the getMinPathSum function and print the result
    cout << sol.minFallingPathSum(matrix) << endl;

    return 0;
}
import java.util.*;

class Solution {
    /* Function to recursively find the
    minimum path sum for a given cell*/
    private int func(int i, int j, int m, int[][] matrix, int[][] dp) {
        // Base Conditions
        if (j < 0 || j >= m)
            return (int) 1e9; 
        if (i == 0)
            return matrix[0][j]; 
        
        /* If the result for this cell is
        already calculated, return it*/
        if (dp[i][j] != -1)
            return dp[i][j];
    
        /* Calculate the minimum path sum by 
        considering three possible directions:
        up, left diagonal, and right diagonal*/
        int up = matrix[i][j] + func(i - 1, j, m, matrix, dp);
        int leftDiagonal = matrix[i][j] + func(i - 1, j - 1, m, matrix, dp);
        int rightDiagonal = matrix[i][j] + func(i - 1, j + 1, m, matrix, dp);
    
        // Store the minimum of the three paths in dp
        return dp[i][j] = Math.min(up, Math.min(leftDiagonal, rightDiagonal));
    }

    // Function to find the minimum path sum in given matrix
    public int minFallingPathSum(int[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;
    
        // Memoization table to store computed results
        int[][] dp = new int[n][m];
        for (int[] row : dp) {
            Arrays.fill(row, -1);
        }
    
        int mini = Integer.MAX_VALUE;
    
        /* Iterate through each cell in the first row to 
        find minimum path sum starting from each of them*/
        for (int j = 0; j < m; j++) {
            int ans = func(n - 1, j, m, matrix, dp);
            mini = Math.min(mini, ans);
        }
        // Return the minimum path sum
        return mini;
    }

    public static void main(String[] args) {
        int[][] matrix = {
            {1, 2, 10, 4},
            {100, 3, 2, 1},
            {1, 1, 20, 2},
            {1, 2, 2, 1}
        };
    
        // Create an instance of Solution class
        Solution sol = new Solution();
    
        // Call the minFallingPathSum function and print the result
        System.out.println(sol.minFallingPathSum(matrix));
    }
}
class Solution:
    """ Function to recursively find the 
    minimum path sum for a given cell"""
    def func(self, i, j, m, matrix, dp):
        # Base Conditions
        if j < 0 or j >= m:
            return int(1e9)
        if i == 0:
            return matrix[0][j]
        
        """ If the result for this cell is
        already calculated, return it"""
        if dp[i][j] != -1:
            return dp[i][j]
    
        """ Calculate the minimum path sum by 
        considering three possible directions:
            up, left diagonal, and right diagonal"""
        up = matrix[i][j] + self.func(i - 1, j, m, matrix, dp)
        left_diagonal = matrix[i][j] + self.func(i - 1, j - 1, m, matrix, dp)
        right_diagonal = matrix[i][j] + self.func(i - 1, j + 1, m, matrix, dp)
    
        # Store the minimum of the three paths in dp
        dp[i][j] = min(up, min(left_diagonal, right_diagonal))
        return dp[i][j]
    
    # Function to find the minimum path sum in given matrix
    def minFallingPathSum(self, matrix):
        n = len(matrix)
        m = len(matrix[0])
    
        # Memoization table to store computed results
        dp = [[-1] * m for _ in range(n)]
    
        mini = float('inf')
    
        """ Iterate through each cell in the first row to
        find minimum path sum starting from each of them"""
        for j in range(m):
            ans = self.func(n - 1, j, m, matrix, dp)
            mini = min(mini, ans)
        
        # Return the minimum path sum
        return mini

if __name__ == "__main__":
    matrix = [
        [1, 2, 10, 4],
        [100, 3, 2, 1],
        [1, 1, 20, 2],
        [1, 2, 2, 1]
    ]
    
    # Create an instance of Solution class
    sol = Solution()
    
    # Call the minFallingPathSum function and print the result
    print(sol.minFallingPathSum(matrix))
class Solution {
    /* Function to recursively find the
    minimum path sum for a given cell*/
    func(i, j, m, matrix, dp) {
        // Base Conditions
        if (j < 0 || j >= m)
            return 1e9;
        if (i === 0)
            return matrix[0][j];
        
        /* If the result for this cell is
        already calculated, return it*/
        if (dp[i][j] !== -1)
            return dp[i][j];
    
        /* Calculate the minimum path sum by 
        considering three possible directions:
        up, left diagonal, and right diagonal*/
        const up = matrix[i][j] + this.func(i - 1, j, m, matrix, dp);
        const leftDiagonal = matrix[i][j] + this.func(i - 1, j - 1, m, matrix, dp);
        const rightDiagonal = matrix[i][j] + this.func(i - 1, j + 1, m, matrix, dp);
    
        // Store the minimum of the three paths in dp
        dp[i][j] = Math.min(up, Math.min(leftDiagonal, rightDiagonal));
        return dp[i][j];
    }
    
    // Function to find the minimum path sum in given matrix
    minFallingPathSum(matrix) {
        const n = matrix.length;
        const m = matrix[0].length;
    
        // Memoization table to store computed results
        const dp = Array.from(Array(n), () => Array(m).fill(-1));
    
        let mini = Infinity;
    
        /* Iterate through each cell in the first row to
        find minimum path sum starting from each of them*/
        for (let j = 0; j < m; j++) {
            const ans = this.func(n - 1, j, m, matrix, dp);
            mini = Math.min(mini, ans);
        }
        
        // Return the minimum path sum
        return mini;
    }
}

const matrix = [
    [1, 2, 10, 4],
    [100, 3, 2, 1],
    [1, 1, 20, 2],
    [1, 2, 2, 1]
];

// Create an instance of Solution class
const sol = new Solution();

// Call the minFallingPathSum function and print the result
console.log(sol.minFallingPathSum(matrix));

Complexity Analysis:

Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. At max, there will be M*N calls of recursion as the subproblems can go upto M*N.

Space Complexity:O((N-1)+(M-1)) + O(M*N), We are using a recursion stack space: O((N-1)+(M-1)), here (N-1)+(M-1) is the path length and an external DP Array of size ‘M*N’.

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

Declare a dp[] array of size [m][n]: As there are two changing parameters(i and j) in the recursive solution, and the maximum value they can attain is (m-1) and (n-1) respectively. So we will require a dp matrix of m*n, where m is total row and n is number of columns. The dp array stores the calculations of subproblems, dp[i][j] represents minimum path sum to reach last row from (i,j).

Setting Base Cases in the Array: In the recursive code, we knew that when i = 0, it means we are at the first row, so the min path from that cell to the firstrow will be the value of that cell itself, so, initialize first row of the dp array to the first row of the input matrix.

Iterative Computation Using Loops: We can use two nested loops to have this traversal. We want to move from the first row to the last row as the 0th row has already been filled for the base case. Whenever we compute values for a cell, we want to have all the values required to calculate it. From the memoized code, it is obvious that the values required for dp[i][j] are dp[i-1][j], dp[i-1][j-1] and dp[i-1][j+1]. So we only need the values from the ‘i-1’ row.

Choosing the minimum: As the question asks for minimum path sum, so update dp[i][j] as the minimum of all the choices.

Returning the last element: At last we need to return the minimum among the last row of dp array as our answer, as the ending cell can be any of the cells from last row.

#include <bits/stdc++.h>
using namespace std;

class Solution{
public:
    /* Function to find the minimum
    path sum in the given matrix*/
    int minFallingPathSum(vector<vector<int>> &matrix) {
        int n = matrix.size(); 
        int m = matrix[0].size(); 

        // Create a 2D DP array to store minimum path sums
        vector<vector<int>> dp(n, vector<int>(m, 0));

        /* Initialize the first row of 
        dp with values from the matrix */
        for (int j = 0; j < m; j++) {
            dp[0][j] = matrix[0][j];
        }

        /* Iterate through the matrix rows
        starting from the second row*/
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < m; j++) {
                /* Calculate the minimum path sum for the
                current cell considering three possible 
                directions: up, left diagonal, and right diagonal*/

                // Up direction
                int up = matrix[i][j] + dp[i - 1][j];

                // Left diagonal direction (if it's a valid move)
                int leftDiagonal = matrix[i][j];
                if (j - 1 >= 0) {
                    leftDiagonal += dp[i - 1][j - 1];
                } else {
                    leftDiagonal += 1e9; 
                }

                // Right diagonal direction 
                int rightDiagonal = matrix[i][j];
                if (j + 1 < m) {
                    rightDiagonal += dp[i - 1][j + 1];
                } else {
                    rightDiagonal += 1e9;  
                }

                // Store the minimum of the three paths in dp
                dp[i][j] = min(up, min(leftDiagonal, rightDiagonal));
            }
        }

        /* Find the minimum value in the last row of dp, which
        represents the minimum path sums ending at each cell*/
        int mini = INT_MAX;
        for (int j = 0; j < m; j++) {
            mini = min(mini, dp[n - 1][j]);
        }

        // Minimum path sum is the minimum value in last row
        return mini;
    }
};

int main() {
    vector<vector<int>> matrix{{1, 2, 10, 4}, {100, 3, 2, 1}, {1, 1, 20, 2}, {1, 2, 2, 1}};
    
    //Create an instance of Solution class
    Solution sol;
    
    // Call the getMinPathSum function and print the result
    cout << sol.minFallingPathSum(matrix) << endl;

    return 0;
}
import java.util.*;

class Solution {
    /* Function to find the minimum
    path sum in the given matrix */
    public int minFallingPathSum(int[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;

        /* Create a 2D DP array to
        store minimum path sums*/
        int[][] dp = new int[n][m];

        /* Initialize the first row of 
        dp with values from the matrix*/
        for (int j = 0; j < m; j++) {
            dp[0][j] = matrix[0][j];
        }

        /* Iterate through the matrix rows
        starting from the second row*/
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < m; j++) {
                /* Calculate the minimum path sum for the
                current cell considering three possible
                directions: up, left diagonal, and right diagonal*/

                // Up direction
                int up = matrix[i][j] + dp[i - 1][j];

                // Left diagonal direction (if it's a valid move)
                int leftDiagonal = matrix[i][j];
                if (j - 1 >= 0) {
                    leftDiagonal += dp[i - 1][j - 1];
                } else {
                    leftDiagonal = Integer.MAX_VALUE;
                }

                // Right diagonal direction
                int rightDiagonal = matrix[i][j];
                if (j + 1 < m) {
                    rightDiagonal += dp[i - 1][j + 1];
                } else {
                    rightDiagonal = Integer.MAX_VALUE; 
                }

                // Store the minimum of the three paths in dp
                dp[i][j] = Math.min(up, Math.min(leftDiagonal, rightDiagonal));
            }
        }

        /* Find the minimum value in the last row of dp, which
        represents the minimum path sums ending at each cell*/
        int mini = Integer.MAX_VALUE;
        for (int j = 0; j < m; j++) {
            mini = Math.min(mini, dp[n - 1][j]);
        }

        // Minimum path sum is the minimum value in last row
        return mini;
    }

    public static void main(String[] args) {
        int[][] matrix = {
            {1, 2, 10, 4},
            {100, 3, 2, 1},
            {1, 1, 20, 2},
            {1, 2, 2, 1}
        };

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the minFallingPathSum function and print the result
        System.out.println(sol.minFallingPathSum(matrix));
    }
}
class Solution:
    def minFallingPathSum(self, matrix):
        n = len(matrix)
        m = len(matrix[0])

        """ Create a 2D DP array to 
        store minimum path sums"""
        dp = [[0] * m for _ in range(n)]

        """ Initialize the first row of dp 
        with values from the matrix"""
        for j in range(m):
            dp[0][j] = matrix[0][j]

        """ Iterate through the matrix rows 
        starting from the second row"""
        for i in range(1, n):
            for j in range(m):
                """ Calculate the minimum path sum for the 
                current cell considering three possible 
                directions: up, left diagonal, and right diagonal"""

                # Up direction
                up = matrix[i][j] + dp[i - 1][j]

                # Left diagonal direction (if it's a valid move)
                left_diagonal = matrix[i][j]
                if j - 1 >= 0:
                    left_diagonal += dp[i - 1][j - 1]
                else:
                    left_diagonal += float('inf')

                # Right diagonal direction
                right_diagonal = matrix[i][j]
                if j + 1 < m:
                    right_diagonal += dp[i - 1][j + 1]
                else:
                    right_diagonal += float('inf')

                # Store the minimum of the three paths in dp
                dp[i][j] = min(up, min(left_diagonal, right_diagonal))

        """ Find the minimum value in the last row of dp, which
        represents the minimum path sums ending at each cell"""
        mini = float('inf')
        for j in range(m):
            mini = min(mini, dp[n - 1][j])

        # Minimum path sum is the minimum value in last row
        return mini

matrix = [
    [1, 2, 10, 4],
    [100, 3, 2, 1],
    [1, 1, 20, 2],
    [1, 2, 2, 1]
]

# Create an instance of Solution class
sol = Solution()

# Call the minFallingPathSum function and print the result
print(sol.minFallingPathSum(matrix))
class Solution {
    /* Function to find the minimum
    path sum in the given matrix */
    minFallingPathSum(matrix) {
        const n = matrix.length;
        const m = matrix[0].length;

        /* Create a 2D DP array to
        store minimum path sums*/
        const dp = Array.from({ length: n }, () => Array(m).fill(0));

        /* Initialize the first row of dp
        with values from the matrix*/
        for (let j = 0; j < m; j++) {
            dp[0][j] = matrix[0][j];
        }

        /* Iterate through the matrix rows
        starting from the second row*/
        for (let i = 1; i < n; i++) {
            for (let j = 0; j < m; j++) {
                /* Calculate the minimum path sum for the
                current cell considering three possible 
                directions: up, left diagonal, and right diagonal*/

                // Up direction
                const up = matrix[i][j] + dp[i - 1][j];

                // Left diagonal direction (if it's a valid move)
                let leftDiagonal = matrix[i][j];
                if (j - 1 >= 0) {
                    leftDiagonal += dp[i - 1][j - 1];
                } else {
                    leftDiagonal += Infinity;
                }

                // Right diagonal direction
                let rightDiagonal = matrix[i][j];
                if (j + 1 < m) {
                    rightDiagonal += dp[i - 1][j + 1];
                } else {
                    rightDiagonal += Infinity;
                }

                // Store the minimum of the three paths in dp
                dp[i][j] = Math.min(up, Math.min(leftDiagonal, rightDiagonal));
            }
        }

        /* Find the minimum value in the last row of dp, which
        represents the minimum path sums ending at each cell*/
        let mini = Infinity;
        for (let j = 0; j < m; j++) {
            mini = Math.min(mini, dp[n - 1][j]);
        }

        // Minimum path sum is the minimum value in last row
        return mini;
    }
}

const matrix = [
    [1, 2, 10, 4],
    [100, 3, 2, 1],
    [1, 1, 20, 2],
    [1, 2, 2, 1]
];

// Create an instance of Solution class
const sol = new Solution();

// Call the minFallingPathSum function and print the result
console.log(sol.minFallingPathSum(matrix));

Complexity Analysis:

Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. As the whole matrix is traversed once using two nested loops.

Space Complexity:O(M*N), As an external DP Array of size ‘M*N’ is used to store the intermediate calculations.

If we observe the relation from tabulation approach, dp[i][j] = matrix[i][j] + min(dp[i-1][j], dp[i-1][j-1], dp[i-1][j+1])). We see that only the previous row is needed, in order to calculate dp[i][j]. Therefore we can space optimize the tabulation approach.

Steps to space optimize the tabulation code:

Initially, take a dummy row ( say prev) and initialize this row to the input matrix's first row( as done in tabulation).
Now the current row(say cur) only needs the prev row’s value inorder to calculate dp[i][j].

At last, we will return the minimum value among the values of the prev row as our answer.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to find the minimum 
    path sum in the given matrix */
    int minFallingPathSum(vector<vector<int>> &matrix) {
        int n = matrix.size(); 
        int m = matrix[0].size(); 
        
        // Represents previous row's minimum path sums
        vector<int> prev(m, 0); 
        
        // Represents current row's minimum path sums
        vector<int> cur(m, 0);  

        // Initialize the first row (base condition)
        for (int j = 0; j < m; j++) {
            prev[j] = matrix[0][j];
        }

        for (int i = 1; i < n; i++) {
            for (int j = 0; j < m; j++) {
                /* Calculate the minimum path sum for the 
                current cell considering three possible 
                directions: up, left diagonal, and right diagonal*/

                // Up direction
                int up = matrix[i][j] + prev[j];

                // Left diagonal direction
                int leftDiagonal = matrix[i][j];
                if (j - 1 >= 0) {
                    leftDiagonal += prev[j - 1];
                } else {
                    leftDiagonal += 1e9; 
                }

                // Right diagonal direction (if it's a valid move)
                int rightDiagonal = matrix[i][j];
                if (j + 1 < m) {
                    rightDiagonal += prev[j + 1];
                } else {
                    rightDiagonal += 1e9; 
                }

                /* Store the minimum of the
                three paths in the current row*/
                cur[j] = min(up, min(leftDiagonal, rightDiagonal));
            }

            /* Update the 'prev' array with the values 
            from the 'cur' array for the next iteration*/
            prev = cur;
        }

        /* Find the minimum value in the last row of 'prev',
        which represents minimum path sums ending at each cell*/
        int mini = INT_MAX;
        for (int j = 0; j < m; j++) {
            mini = min(mini, prev[j]);
        }

        /* The minimum path sum is the minimum
        value in the last row of 'prev'*/
        return mini;
    }
};

int main() {
    vector<vector<int>> matrix{
        {1, 2, 10, 4},
        {100, 3, 2, 1},
        {1, 1, 20, 2},
        {1, 2, 2, 1}
    };
    
    // Create an instance of Solution class
    Solution sol;
    
    // Call the minFallingPathSum function and print the result
    cout << sol.minFallingPathSum(matrix) << endl;

    return 0;
}
import java.util.*;

class Solution {
    /* Function to find the minimum
    path sum in the given matrix */
    public int minFallingPathSum(int[][] matrix) {
        int n = matrix.length;
        int m = matrix[0].length;

        // Represents previous row's minimum path sums
        int[] prev = new int[m];

        // Represents current row's minimum path sums
        int[] cur = new int[m];

        // Initialize the first row (base condition)
        for (int j = 0; j < m; j++) {
            prev[j] = matrix[0][j];
        }

        for (int i = 1; i < n; i++) {
            for (int j = 0; j < m; j++) {
                /* Calculate the minimum path sum for the
                current cell considering three possible
                directions: up, left diagonal, and right diagonal */

                // Up direction
                int up = matrix[i][j] + prev[j];

                // Left diagonal direction
                int leftDiagonal = matrix[i][j];
                if (j - 1 >= 0) {
                    leftDiagonal += prev[j - 1];
                } else {
                    leftDiagonal = Integer.MAX_VALUE;
                }

                // Right diagonal direction
                int rightDiagonal = matrix[i][j];
                if (j + 1 < m) {
                    rightDiagonal += prev[j + 1];
                } else {
                    rightDiagonal = Integer.MAX_VALUE;
                }

                /* Store the minimum of the
                three paths in the current row */
                cur[j] = Math.min(up, Math.min(leftDiagonal, rightDiagonal));
            }

            /* Update the 'prev' array with the values
            from the 'cur' array for the next iteration */
            System.arraycopy(cur, 0, prev, 0, m);
        }

        /* Find the minimum value in the last row of 'prev',
        which represents minimum path sums ending at each cell */
        int mini = Integer.MAX_VALUE;
        for (int j = 0; j < m; j++) {
            mini = Math.min(mini, prev[j]);
        }

        /* The minimum path sum is the minimum
        value in the last row of 'prev' */
        return mini;
    }

    public static void main(String[] args) {
        int[][] matrix = {
            {1, 2, 10, 4},
            {100, 3, 2, 1},
            {1, 1, 20, 2},
            {1, 2, 2, 1}
        };

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Call the minFallingPathSum function and print the result
        System.out.println(sol.minFallingPathSum(matrix));
    }
}
class Solution:
    """ Function to find the minimum
    path sum in the given matrix """
    def minFallingPathSum(self, matrix):
        n = len(matrix)
        m = len(matrix[0])
        
        # Represents previous row's minimum path sums
        prev = [0] * m
        
        # Represents current row's minimum path sums
        cur = [0] * m

        # Initialize the first row (base condition)
        for j in range(m):
            prev[j] = matrix[0][j]

        for i in range(1, n):
            for j in range(m):
                """ Calculate the minimum path sum for the
                current cell considering three possible 
                directions: up, left diagonal, and right diagonal"""

                # Up direction
                up = matrix[i][j] + prev[j]

                # Left diagonal direction
                leftDiagonal = matrix[i][j]
                if j - 1 >= 0:
                    leftDiagonal += prev[j - 1]
                else:
                    leftDiagonal += float('inf')

                # Right diagonal direction
                rightDiagonal = matrix[i][j]
                if j + 1 < m:
                    rightDiagonal += prev[j + 1]
                else:
                    rightDiagonal += float('inf')

                """ Store the minimum of the 
                three paths in the current row"""
                cur[j] = min(up, min(leftDiagonal, rightDiagonal))

            """ Update the 'prev' array with the values
            from the 'cur' array for the next iteration"""
            prev = cur[:]

        """ Find the minimum value in the last row of 'prev',
        which represents minimum path sums ending at each cell"""
        mini = float('inf')
        for j in range(m):
            mini = min(mini, prev[j])

        """ The minimum path sum is the minimum
        value in the last row of 'prev'"""
        return mini

if __name__ == "__main__":
    matrix = [
        [1, 2, 10, 4],
        [100, 3, 2, 1],
        [1, 1, 20, 2],
        [1, 2, 2, 1]
    ]

    # Create an instance of Solution class
    sol = Solution()

    # Call the minFallingPathSum function and print the result
    print(sol.minFallingPathSum(matrix))
class Solution {
    /* Function to find the minimum
    path sum in the given matrix */
    minFallingPathSum(matrix) {
        let n = matrix.length;
        let m = matrix[0].length;

        // Represents previous row's minimum path sums
        let prev = new Array(m).fill(0);

        // Represents current row's minimum path sums
        let cur = new Array(m).fill(0);

        // Initialize the first row (base condition)
        for (let j = 0; j < m; j++) {
            prev[j] = matrix[0][j];
        }

        for (let i = 1; i < n; i++) {
            for (let j = 0; j < m; j++) {
                /* Calculate the minimum path sum for the 
                current cell considering three possible 
                directions: up, left diagonal, and right diagonal*/

                // Up direction
                let up = matrix[i][j] + prev[j];

                // Left diagonal direction
                let leftDiagonal = matrix[i][j];
                if (j - 1 >= 0) {
                    leftDiagonal += prev[j - 1];
                } else {
                    leftDiagonal += Number.POSITIVE_INFINITY;
                }

                // Right diagonal direction
                let rightDiagonal = matrix[i][j];
                if (j + 1 < m) {
                    rightDiagonal += prev[j + 1];
                } else {
                    rightDiagonal += Number.POSITIVE_INFINITY;
                }

                /* Store the minimum of the 
                three paths in the current row*/
                cur[j] = Math.min(up, Math.min(leftDiagonal, rightDiagonal));
            }

            /* Update the 'prev' array with the values from 
            the 'cur' array for the next iteration*/
            prev = cur.slice();
        }

        /* Find the minimum value in the last row of 'prev',
        which represents minimum path sums ending at each cell*/
        let mini = Number.POSITIVE_INFINITY;
        for (let j = 0; j < m; j++) {
            mini = Math.min(mini, prev[j]);
        }

        /* The minimum path sum is the minimum
        value in the last row of 'prev'*/
        return mini;
    }
}

const matrix = [
    [1, 2, 10, 4],
    [100, 3, 2, 1],
    [1, 1, 20, 2],
    [1, 2, 2, 1]
];

// Create an instance of Solution class
const sol = new Solution();

// Call the minFallingPathSum function and print the result
console.log(sol.minFallingPathSum(matrix));

Complexity Analysis:

Time Complexity: O(M*N), where M is the number of row and N is the number of column in 2D array. As the whole matrix is traversed once using two nested loops.

Space Complexity:O(M), As an external array of size ‘M’ is used to store only one row.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Why Greedy Approach will not work:

Steps to form the recursive solution:

Complexity Analysis:

Complexity Analysis:

Complexity Analysis:

Steps to space optimize the tabulation code:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code