Search in BST

Binary Search Trees Theory and Basics Easy

Searching for a specific node in a binary search tree (BST) is a fundamental function that underlies many real-world applications, including database management systems and search engines
These systems often use a form of BST known as a B-tree
When you perform a Google search or a SQL query, these systems are using a version of the search operation defined in this problem to efficiently find relevant records among possibly billions
This is because BST allow for efficient lookups, additions, and deletions, which are key operations for these systems

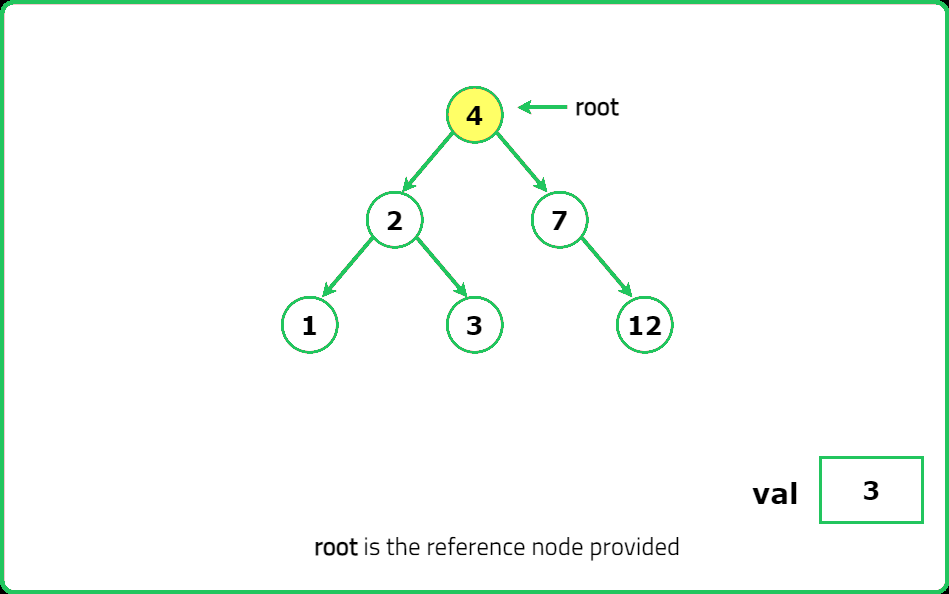
Given the root of a binary search tree (BST) and an integer val.

Find the node in the BST that the node's value equals val and return the subtree rooted with that node. If such a node does not exist, return null.

Examples:

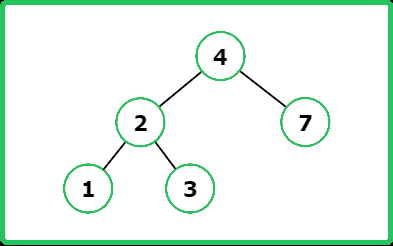
Input : root = [4, 2, 7, 1, 3] , val = 2

Output : [2, 1, 3]

Explanation :

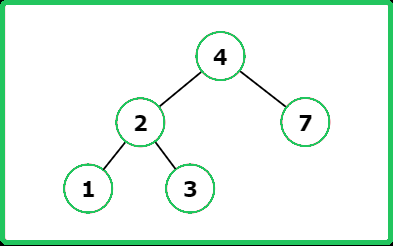
Input : root = [4, 2, 7, 1, 3] , val = 5

Output : []

Explanation :

Input : root = [10, 2, 12, 1, 4, null, null, null, null, 3] , val = 2

Constraints

1 <= Number of Nodes <= 5000
1 <= Node.val <= 10⁷
1 <= val <= 10⁷
All nodes values in BST are unique.

Hints

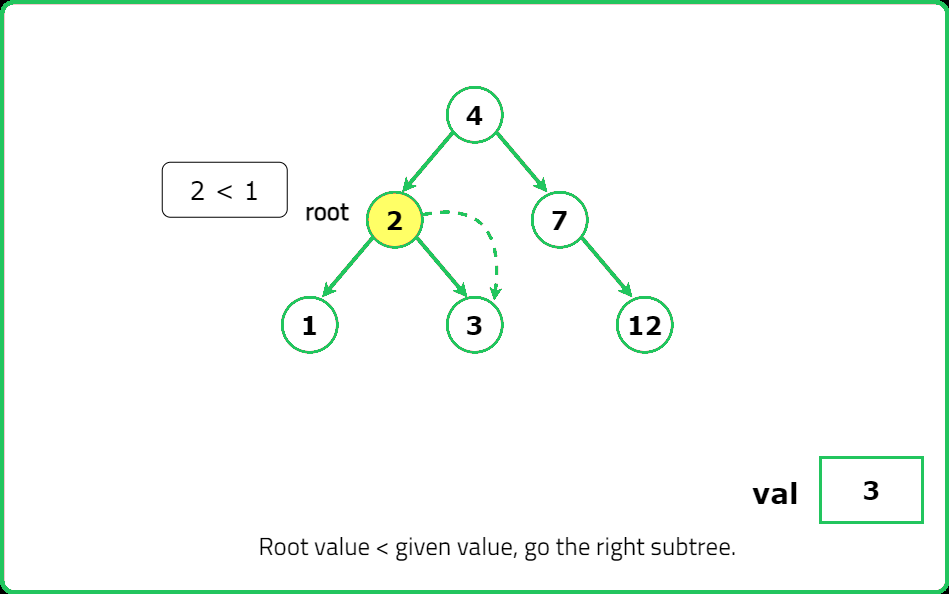
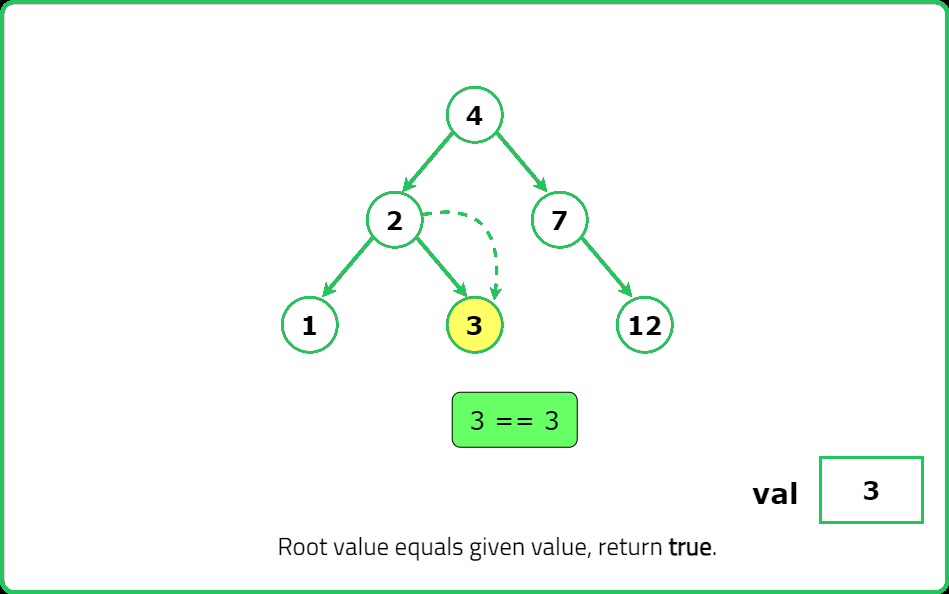
If val == root.val, return the subtree rooted at this node. If val < root.val, recursively search in the left subtree. If val > root.val, recursively search in the right subtree.
If val matches the current node, return it. If val < root.val, move to the left subtree. If val > root.val, move to the right subtree. If null is reached, return null (value not found).

Company Tags

Visa Bain & Company Salesforce GE Healthcare Byju's Alibaba Lyft eBay Databricks Siemens Healthineers Splunk IBM Mastercard Etsy Roblox Epic Games PayPal PwC Docker Zomato Dropbox Twilio Johnson & Johnson AMD OYO Rooms Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

              document.body.innerHTML = '';
              const iframeHTML = `
                <div style="padding-top:56.25%;position:relative;">
                  <iframe 
                    src="https://app.tpstreams.com/embed/atsjxr/4uXKEhXM4DQ/?access_token=33e345b1-9f22-4382-8c5c-7e49a75d8027" 
                    style="border:0;max-width:100%;position:absolute;top:0;left:0;height:100%;width:100%;" 
                    allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" 
                    allowfullscreen="" 
                    frameborder="0">
                  </iframe>
                </div>
              `;
              document.body.innerHTML = iframeHTML;
              
              const script = document.createElement('script');
              script.src = 'https://static.testpress.in/static/js/player.js';
              document.head.appendChild(script);
              
              script.onload = () => {
                const iframe = document.querySelector('iframe');
                const player = new Testpress.Player(iframe);
              
                player.loaded().then(() => {
                  console.log('Player is ready now');
                });
              
                player.on('play', () => {
                  console.log('Played the video');
                });
              };

Intuition

In a Binary Search Tree (BST), the key property is that for any given node N, all nodes in its left subtree contain values smaller than N, while all nodes in its right subtree hold values greater than N. This structure facilitates an efficient search for a value X, which can be understood through three distinct scenarios:

1. If the value at node N matches X, then N is the target node.

2. If the value at node N is less than X, the search must proceed to the right subtree, as X cannot exist in the left subtree.

3. If the value at node N is greater than X, the search must continue in the left subtree, since X cannot be found in the right subtree.

Approach

Initiate a traversal of the tree using a while loop, conditioned on the root being non-NULL and the root's data not matching X.
If the root's data is less than X, shift the focus to the right child of the root.
If the root's data exceeds X, redirect the search to the left child of the root.
Upon exiting the loop, if the root is NULL, it indicates that X is not present in the tree, and the function should return NULL. Otherwise, return the node containing the value X.

Dry Run

Solution

//  Definition for a binary tree node.
struct TreeNode {
      int data;
      TreeNode *left;
      TreeNode *right;
      TreeNode(int val) : data(val), left(nullptr), right(nullptr) {}
  };
 
class Solution {	
public:	
    TreeNode* searchBST(TreeNode* root, int val) {
        // Traverse the tree until we find the node 
        // with the given value or reach the end
        while (root != nullptr && root->data != val) {
            // Move to the left or right child 
           // depending on the value comparison
            root = (root->data > val) ? root->left : root->right;
        }
        // Return the found node or nullptr if not found
        return root; 
    }
};

// Example usage
int main() {
    // Creating a simple BST for demonstration
    TreeNode* root = new TreeNode(4);
    root->left = new TreeNode(2);
    root->right = new TreeNode(7);
    root->left->left = new TreeNode(1);
    root->left->right = new TreeNode(3);

    Solution sol;
    TreeNode* result = sol.searchBST(root, 2);
    if (result) {
        std::cout << "Node found with value: " << result->data << std::endl;
    } else {
        std::cout << "Node not found" << std::endl;
    }

    // Clean up memory (omitted for brevity)
    return 0;
}
// Definition for a binary tree node.
public class TreeNode {
      int data;
      TreeNode left;
      TreeNode right;
      TreeNode(int val) { data = val; left = null; right = null; }
  }
 

class Solution {
    public TreeNode searchBST(TreeNode root, int val) {
        // Traverse the tree until we find the node 
       // with the given value or reach the end
        while (root != null && root.data != val) {
            // Move to the left or right child 
            // depending on the value comparison
            root = (root.data > val) ? root.left : root.right;
        }
       // Return the found node or null if not found
        return root; 
    }

    // Example usage
    public static void main(String[] args) {
        // Creating a simple BST for demonstration
        TreeNode root = new TreeNode(4);
        root.left = new TreeNode(2);
        root.right = new TreeNode(7);
        root.left.left = new TreeNode(1);
        root.left.right = new TreeNode(3);

        Solution sol = new Solution();
        TreeNode result = sol.searchBST(root, 2);
        if (result != null) {
            System.out.println("Node found with value: " + result.data);
        } else {
            System.out.println("Node not found");
        }
    }
}
# Definition for a binary tree node.
class TreeNode(object):
     def __init__(self, val=0, left=None, right=None):
         self.data = val
         self.left = left
         self.right = right

class Solution:
    def searchBST(self, root, val):
        # Traverse the tree until we find the node 
        # with the given value or reach the end
        while root is not None and root.data != val:
            # Move to the left or right child 
           # depending on the value comparison
            root = root.left if root.data > val else root.right
        # Return the found node or None if not found
        return root  

# Example usage
def main():
    # Creating a simple BST for demonstration
    root = TreeNode(4)
    root.left = TreeNode(2)
    root.right = TreeNode(7)
    root.left.left = TreeNode(1)
    root.left.right = TreeNode(3)

    sol = Solution()
    result = sol.searchBST(root, 2)
    if result:
        print(f"Node found with value: {result.data}")
    else:
        print("Node not found")

if __name__ == "__main__":
    main()
// Definition for a binary tree node.
class TreeNode {
      constructor(val = 0, left = null, right = null) {
          this.data = val;
          this.left = left;
          this.right = right;
      }
 }
 
class Solution {
    searchBST(root, val) {
        // Traverse the tree until we find the node 
       // with the given value or reach the end
        while (root !== null && root.data !== val) {
            // Move to the left or right child 
           // depending on the value comparison
            root = (root.data > val) ? root.left : root.right;
        }
       // Return the found node or null if not found
        return root; 
    }
}

// Example usage
function main() {
    // Creating a simple BST for demonstration
    let root = new TreeNode(4);
    root.left = new TreeNode(2);
    root.right = new TreeNode(7);
    root.left.left = new TreeNode(1);
    root.left.right = new TreeNode(3);

    let sol = new Solution();
    let result = sol.searchBST(root, 2);
    if (result) {
        console.log("Node found with value: " + result.data);
    } else {
        console.log("Node not found");
    }
}

main();

Complexity Analysis

Time Complexity: O(log₂(N)) : The time complexity is O(log2(N)) in a balanced BST since the search space is halved at each step. However, in the worst case (skewed tree), it can be O(N).

Space Complexity: O(1): The space complexity is O(1) as the search is performed iteratively without using additional space.

Code

Problem List