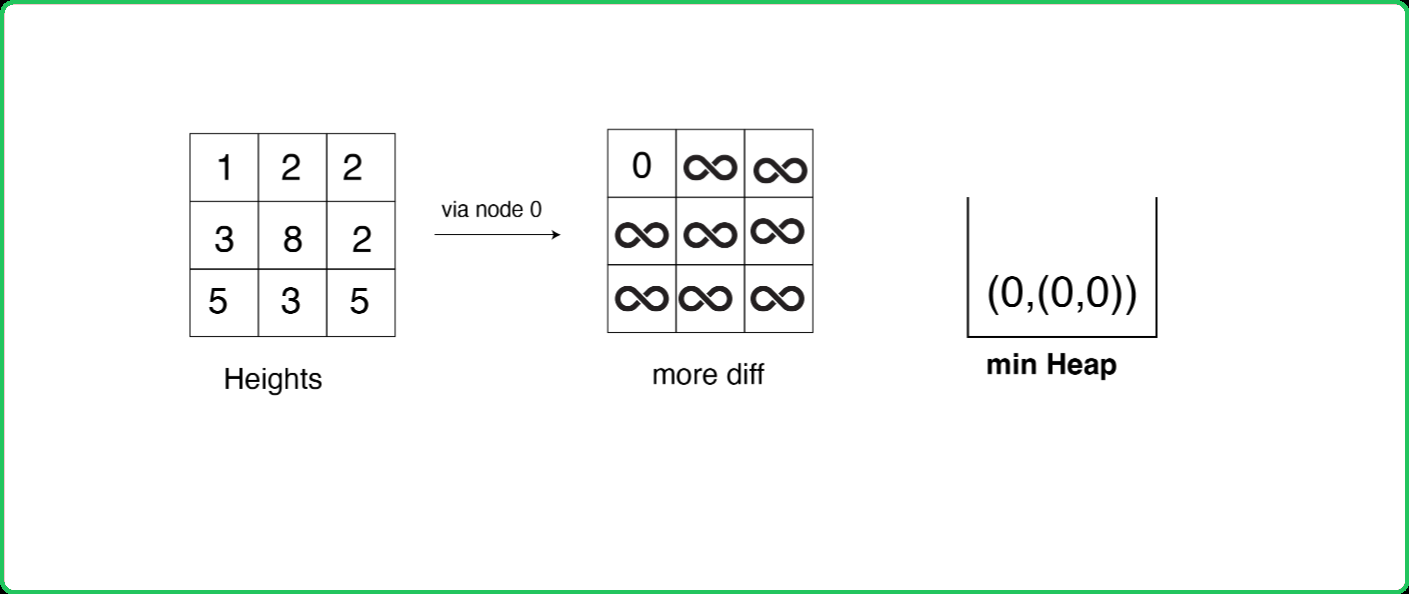
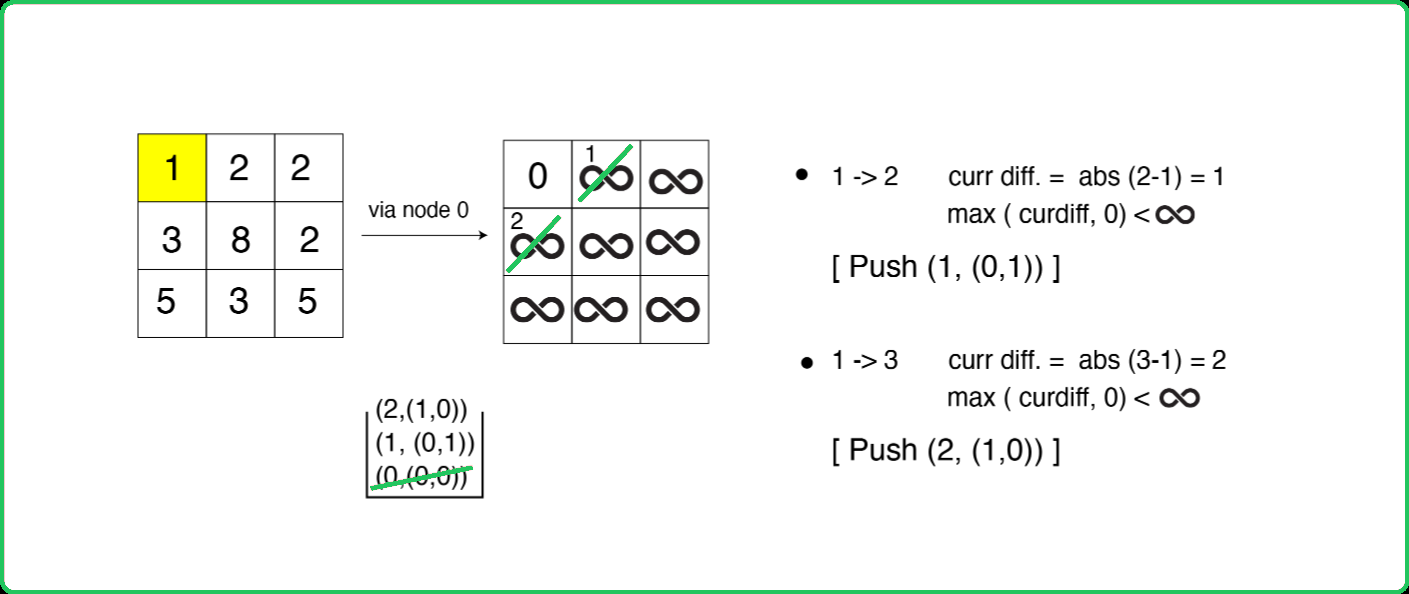
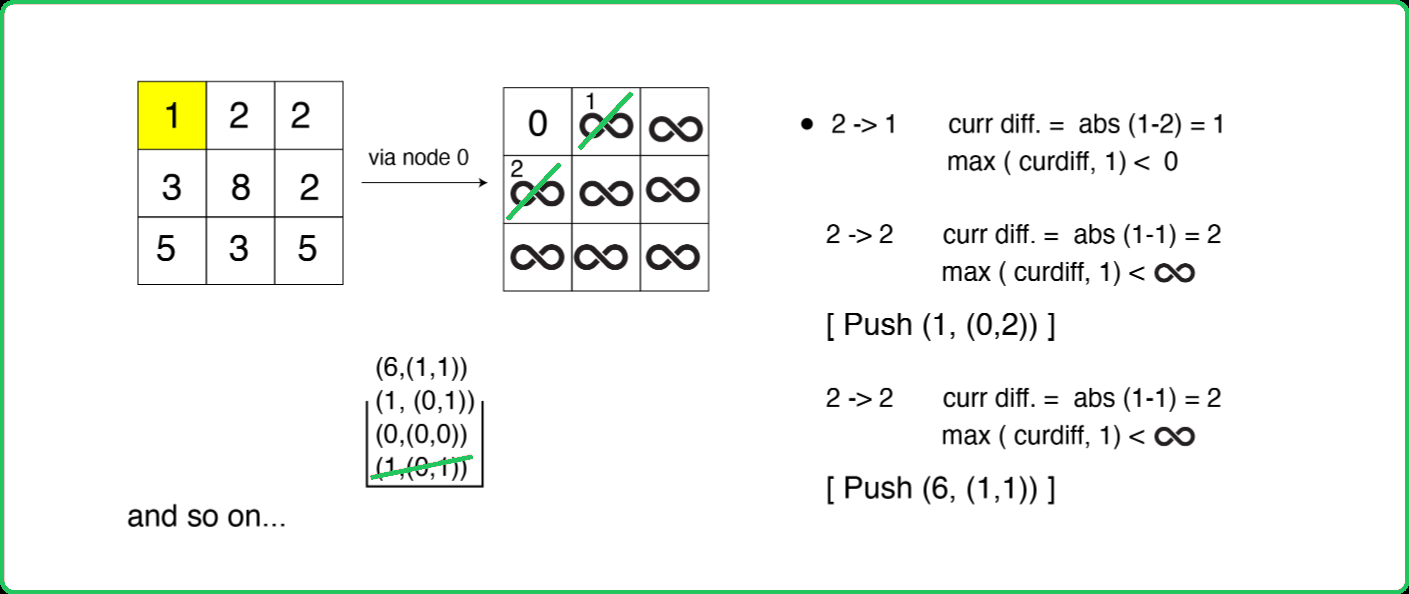
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124
#include <bits/stdc++.h>
using namespace std;
/* Define P as a shorthand for
the pair<int, pair<int,int>> type */
#define P pair <int, pair<int,int>>
class Solution {
private:
// Delta row and column array
vector<int> delRow = {-1, 0, 1, 0};
vector<int> delCol = {0, -1, 0, 1};
// Function to check if a cell is valid
bool isValid(int &row, int &col,
int &n, int &m) {
// Return false if the cell is invalid
if(row < 0 || row >= n) return false;
if(col < 0 || col >= m) return false;
// Return true if the cell is valid
return true;
}
public:
/* Function to determine minimum efforts
to go from top-left to bottom-right */
int MinimumEffort(vector<vector<int>>& heights) {
// Get the dimensions of grid
int n = heights.size();
int m = heights[0].size();
// To store maximum difference
vector<vector<int>> maxDiff(n, vector<int>(m, 1e9));
/* Min-Heap storing the pair:
{diff, {row of cell, column of cell}} */
priority_queue <P, vector<P>, greater<P>> pq;
// Mark the initial position as 0
maxDiff[0][0] = 0;
// Push the starting cell to min-heap
pq.push({0, {0, 0}});
// Until the min-heap is not empty
while(!pq.empty()) {
/* Get the cell with minimum
difference (effort) */
auto p = pq.top();
// Get the difference
int diff = p.first;
int row = p.second.first; // Row
int col = p.second.second; // Column
pq.pop();
/* If the destination cell is reached,
return the difference */
if(row == n-1 && col == m-1)
return diff;
// Traverse it's neighbors
for(int i=0; i<4; i++) {
/* Get the coordinates
of neighboring cell */
int newRow = row + delRow[i];
int newCol = col + delCol[i];
// Check if the cell is valid
if(isValid(newRow, newCol, n, m)) {
/* Get the current difference
in heights of cells */
int currDiff =
abs(heights[newRow][newCol] - heights[row][col]);
/* Check if the current difference is
less than earlier known difference */
if(max(currDiff, diff) < maxDiff[newRow][newCol]) {
// Store the current difference
maxDiff[newRow][newCol] = max(currDiff, diff);
// Add the new pair found in the min-heap
pq.push({max(currDiff, diff), {newRow, newCol}});
}
}
}
}
// Return -1
return -1;
}
};
int main() {
vector<vector<int>> heights = {
{1,2,2},
{3,8,2},
{5,3,5}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to determine minimum efforts
to go from top-left to bottom-right */
int ans = sol.MinimumEffort(heights);
// Output
cout << "The minimum efforts required to go from cell (0,0) to cell (row-1, col-1) is: " << ans;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113
import java.util.*;
class Solution {
// Delta row and column array
int[] delRow = {-1, 0, 1, 0};
int[] delCol = {0, -1, 0, 1};
// Function to check if a cell is valid
boolean isValid(int row, int col, int n, int m) {
// Return false if the cell is invalid
if (row < 0 || row >= n) return false;
if (col < 0 || col >= m) return false;
// Return true if the cell is valid
return true;
}
/* Function to determine minimum efforts
to go from top-left to bottom-right */
public int MinimumEffort(List<List<Integer>> heights) {
// Get the dimensions of grid
int n = heights.size();
int m = heights.get(0).size();
// To store maximum difference
int[][] maxDiff = new int[n][m];
for (int[] row : maxDiff)
Arrays.fill(row, Integer.MAX_VALUE);
/* Min-Heap storing the pair:
{diff, {row of cell, column of cell}} */
PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
// Mark the initial position as 0
maxDiff[0][0] = 0;
// Push the starting cell to min-heap
pq.add(new int[]{0, 0, 0});
// Until the min-heap is not empty
while (!pq.isEmpty()) {
/* Get the cell with minimum
difference (effort) */
int[] p = pq.poll();
// Get the difference
int diff = p[0];
int row = p[1]; // Row
int col = p[2]; // Column
/* If the destination cell is reached,
return the difference */
if (row == n - 1 && col == m - 1)
return diff;
// Traverse its neighbors
for (int i = 0; i < 4; i++) {
/* Get the coordinates
of neighboring cell */
int newRow = row + delRow[i];
int newCol = col + delCol[i];
// Check if the cell is valid
if (isValid(newRow, newCol, n, m)) {
/* Get the current difference
in heights of cells */
int currDiff = Math.abs(heights.get(newRow).get(newCol) - heights.get(row).get(col));
/* Check if the current difference is
less than earlier known difference */
if (Math.max(currDiff, diff) < maxDiff[newRow][newCol]) {
// Store the current difference
maxDiff[newRow][newCol] = Math.max(currDiff, diff);
// Add the new pair found in the min-heap
pq.add(new int[]{Math.max(currDiff, diff), newRow, newCol});
}
}
}
}
// Return -1
return -1;
}
public static void main(String[] args) {
List<List<Integer>> heights = Arrays.asList(
Arrays.asList(1, 2, 2),
Arrays.asList(3, 8, 2),
Arrays.asList(5, 3, 5)
);
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to determine minimum efforts
to go from top-left to bottom-right */
int ans = sol.MinimumEffort(heights);
// Output
System.out.println("The minimum efforts required to go from cell (0,0) to cell (row-1, col-1) is: " + ans);
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495969798
import heapq
class Solution:
# Delta row and column array
delRow = [-1, 0, 1, 0]
delCol = [0, -1, 0, 1]
# Function to check if a cell is valid
def isValid(self, row, col, n, m):
# Return false if the cell is invalid
if row < 0 or row >= n: return False
if col < 0 or col >= m: return False
# Return true if the cell is valid
return True
# Function to determine minimum efforts
# to go from top-left to bottom-right
def MinimumEffort(self, heights):
# Get the dimensions of grid
n = len(heights)
m = len(heights[0])
# To store maximum difference
maxDiff = [[float('inf')] * m for _ in range(n)]
# Min-Heap storing the pair:
# {diff, {row of cell, column of cell}}
pq = []
# Mark the initial position as 0
maxDiff[0][0] = 0
# Push the starting cell to min-heap
heapq.heappush(pq, (0, 0, 0))
# Until the min-heap is not empty
while pq:
# Get the cell with minimum
# difference (effort)
diff, row, col = heapq.heappop(pq)
# If the destination cell is reached,
# return the difference
if row == n-1 and col == m-1:
return diff
# Traverse its neighbors
for i in range(4):
# Get the coordinates
# of neighboring cell
newRow = row + self.delRow[i]
newCol = col + self.delCol[i]
# Check if the cell is valid
if self.isValid(newRow, newCol, n, m):
# Get the current difference
# in heights of cells
currDiff = abs(heights[newRow][newCol] -
heights[row][col])
# Check if the current difference is
# less than earlier known difference
if (max(currDiff, diff) <
maxDiff[newRow][newCol]):
# Store the current difference
maxDiff[newRow][newCol] = max(currDiff, diff)
# Add the new pair found in the min-heap
heapq.heappush(pq, (max(currDiff, diff), newRow, newCol))
# Return -1
return -1
# Example usage
if __name__ == "__main__":
heights = [
[1, 2, 2],
[3, 8, 2],
[5, 3, 5]
]
# Creating an instance of Solution class
sol = Solution()
# Function call to determine minimum efforts
# to go from top-left to bottom-right
ans = sol.MinimumEffort(heights)
# Output
print(f"The minimum efforts required to go from cell (0,0) to cell (row-1, col-1) is: {ans}")
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182
// Min-Heap Class implementation
class MinHeap {
constructor() {
this.heap = [];
}
// Insert a new value into the heap
push(val) {
this.heap.push(val);
this.bubbleUp();
}
// Remove and return the smallest value from the heap
pop() {
if (this.size() === 1) return this.heap.pop();
const min = this.heap[0];
this.heap[0] = this.heap.pop();
this.bubbleDown();
return min;
}
// Return the smallest value from the heap
peek() {
return this.heap[0];
}
// Return the number of elements in the heap
size() {
return this.heap.length;
}
// Bubble up the newly added value to maintain heap property
bubbleUp() {
let index = this.heap.length - 1;
while (index > 0) {
const parentIndex = Math.floor((index - 1) / 2);
if (this.heap[index][0] >= this.heap[parentIndex][0]) break;
[this.heap[index], this.heap[parentIndex]] = [this.heap[parentIndex], this.heap[index]];
index = parentIndex;
}
}
// Bubble down the top value to maintain heap property
bubbleDown() {
let index = 0;
const length = this.heap.length;
const element = this.heap[0];
while (true) {
let leftChildIndex = 2 * index + 1;
let rightChildIndex = 2 * index + 2;
let leftChild, rightChild;
let swapIndex = null;
if (leftChildIndex < length) {
leftChild = this.heap[leftChildIndex];
if (leftChild[0] < element[0]) {
swapIndex = leftChildIndex;
}
}
if (rightChildIndex < length) {
rightChild = this.heap[rightChildIndex];
if (
(swapIndex === null && rightChild[0] < element[0]) ||
(swapIndex !== null && rightChild[0] < leftChild[0])
) {
swapIndex = rightChildIndex;
}
}
if (swapIndex === null) break;
this.heap[index] = this.heap[swapIndex];
this.heap[swapIndex] = element;
index = swapIndex;
}
}
}
class Solution {
constructor() {
// Delta row and column array
this.delRow = [-1, 0, 1, 0];
this.delCol = [0, -1, 0, 1];
}
// Function to check if a cell is valid
isValid(row, col, n, m) {
// Return false if the cell is invalid
if (row < 0 || row >= n) return false;
if (col < 0 || col >= m) return false;
// Return true if the cell is valid
return true;
}
/* Function to determine minimum efforts
to go from top-left to bottom-right */
MinimumEffort(heights) {
// Get the dimensions of grid
const n = heights.length;
const m = heights[0].length;
// To store maximum difference
const maxDiff = Array.from(
{ length: n },
() => Array(m).fill(Infinity)
);
/* Min-Heap storing the pair:
{diff, {row of cell, column of cell}} */
const pq = new MinHeap();
// Mark the initial position as 0
maxDiff[0][0] = 0;
// Push the starting cell to min-heap
pq.push([0, 0, 0]);
// Until the min-heap is not empty
while (pq.size() > 0) {
/* Get the cell with minimum
difference (effort) */
const [diff, row, col] = pq.pop();
/* If the destination cell is reached,
return the difference */
if (row === n - 1 && col === m - 1)
return diff;
// Traverse its neighbors
for (let i = 0; i < 4; i++) {
/* Get the coordinates
of neighboring cell */
const newRow = row + this.delRow[i];
const newCol = col + this.delCol[i];
// Check if the cell is valid
if (this.isValid(newRow, newCol, n, m)) {
/* Get the current difference
in heights of cells */
const currDiff =
Math.abs(heights[newRow][newCol] - heights[row][col]);
/* Check if the current difference is
less than earlier known difference */
if (Math.max(currDiff, diff) <
maxDiff[newRow][newCol]) {
// Store the current difference
maxDiff[newRow][newCol] =
Math.max(currDiff, diff);
// Add the new pair found in the min-heap
pq.push(
[Math.max(currDiff, diff),
newRow, newCol]
);
}
}
}
}
// Return -1
return -1;
}
}
// Example usage
const heights = [
[1, 2, 2],
[3, 8, 2],
[5, 3, 5]
];
/* Creating an instance of
Solution class */
const sol = new Solution();
/* Function call to determine minimum efforts
to go from top-left to bottom-right */
const ans = sol.MinimumEffort(heights);
// Output
console.log(`The minimum efforts required to go from cell (0,0) to cell (row-1, col-1) is: ${ans}`);