Requirements needed to construct a unique BT
Binary Trees
Construction Problems
Hard
Given a pair of tree traversal, return true if a unique binary tree can be constructed otherwise false. Each traversal is represented with integer: 1 -> Preorder , 2 -> Inorder , 3 -> Postorder.
Examples:
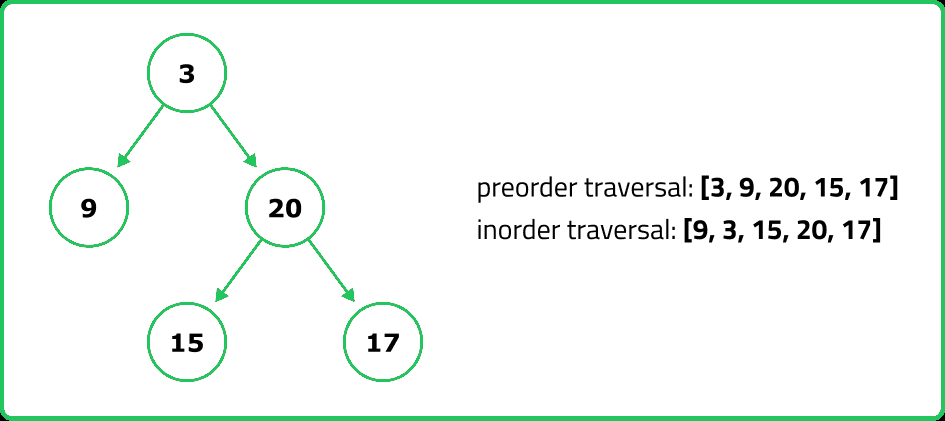
Input : 1 2
Output : true
Explanation : Answer is True.
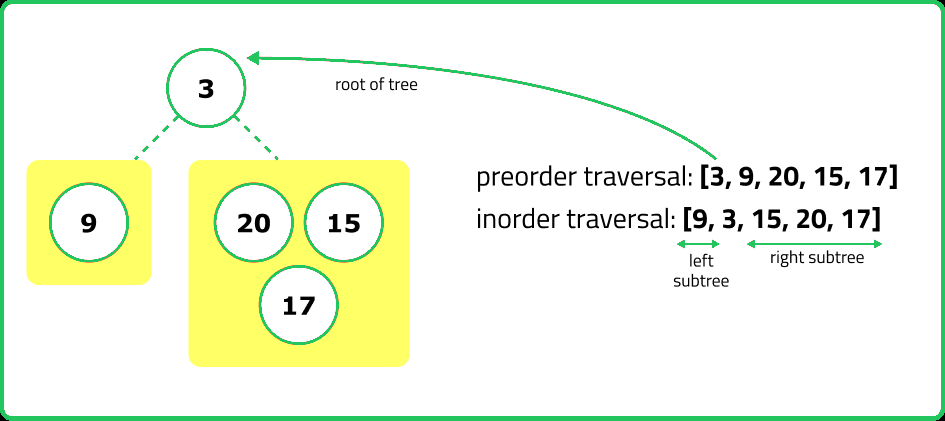
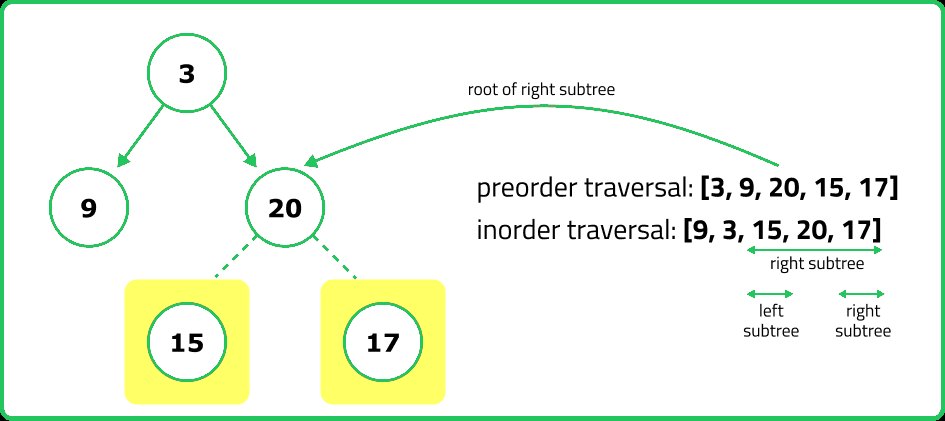
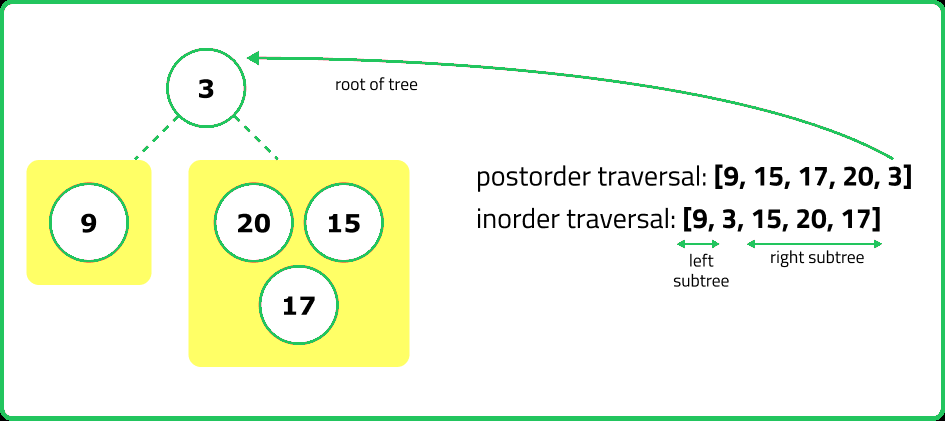
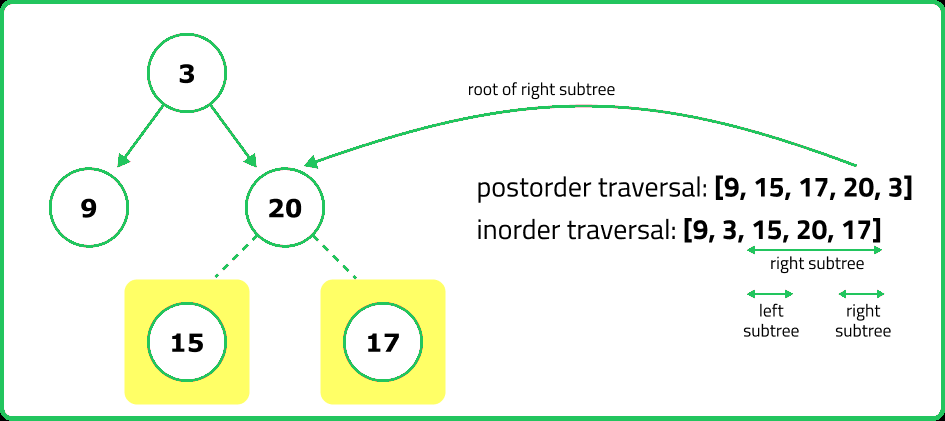
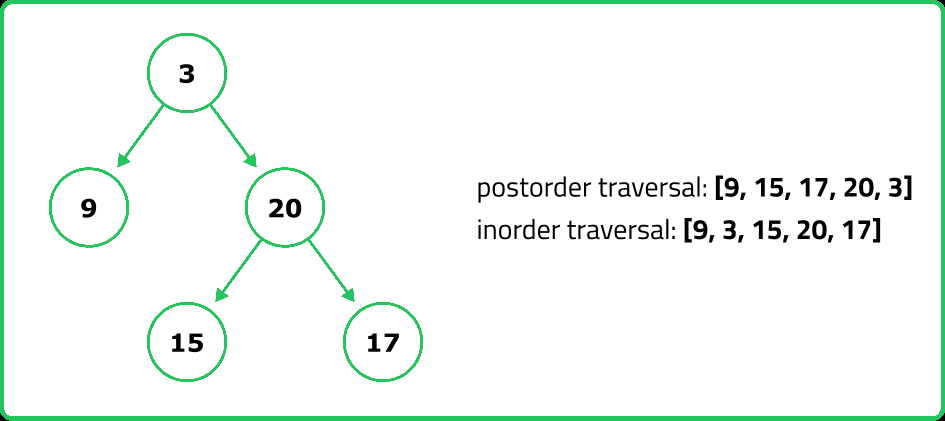
It is possible to construct a unique binary tree. This is because the preorder traversal provides the root of the tree, and the inorder traversal helps determine the left and right subtrees.
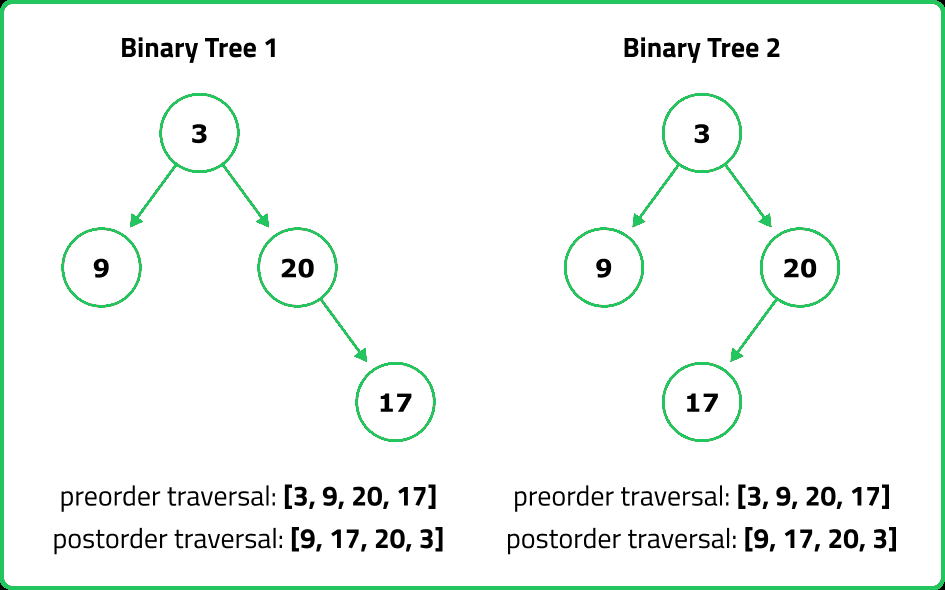
Input : 2 2
Output : false
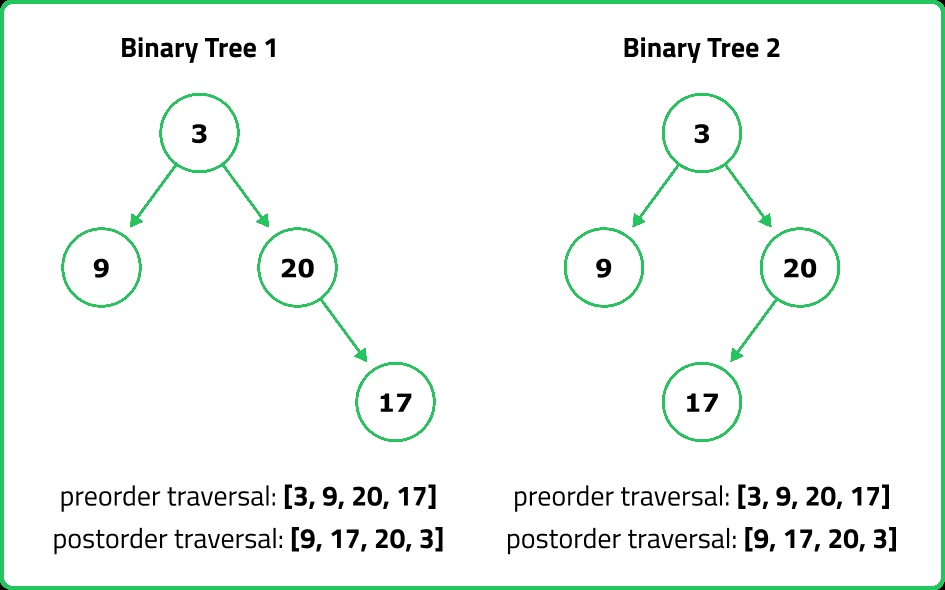
Explanation : Two inorder traversals are insufficient to uniquely determine a binary tree.
Input : 1 3
Constraints
- 1 <= a, b <= 3
Hints
- Given two types of tree traversals, we need to determine if a unique binary tree can be reconstructed. Each traversal is represented by an integer identifier 1 → Preorder Traversal 2 → Inorder Traversal 3 → Postorder Traversal
- A binary tree can only be uniquely constructed if: One of the traversals must be Inorder, because Inorder preserves the relative position of nodes. The second traversal must be either Preorder or Postorder
Company Tags
Roche
Zomato
Alibaba
McKinsey & Company
Micron Technology
Medtronic
AMD
Deloitte
GE Healthcare
Epic Games
Oracle
Swiggy
Uber
Freshworks
Wayfair
Databricks
IBM
ARM
Johnson & Johnson
DoorDash
Robinhood
Ernst & Young
NVIDIA
Zynga
Bloomberg
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe