Lower Bound
Binary Search
Fundamentals
Easy
- Fun Fact: Lower bound algorithms are commonly used in database queries and search engines
- They help improve the speed of searches by eliminating sections of data that don't need to be searched
- For example, when you're typing in the search bar of an e-commerce app, a lower bound algorithm can quickly find the starting point of the products that start with the letters you've entered, significantly speeding up the search process
- So, every time you search for a product on a shopping app or a keyword on a search engine, there's a good chance you're using a lower bound algorithm!
Given a sorted array of nums and an integer x, write a program to find the lower bound of x. The lower bound algorithm finds the first or the smallest index in a sorted array where the value at that index is greater than or equal to a given key i.e. x.
If no such index is found, return the size of the array.
Examples:
Input : nums= [1,2,2,3], x = 2
Output:1
Explanation: Index 1 is the smallest index such that arr[1] >= x.
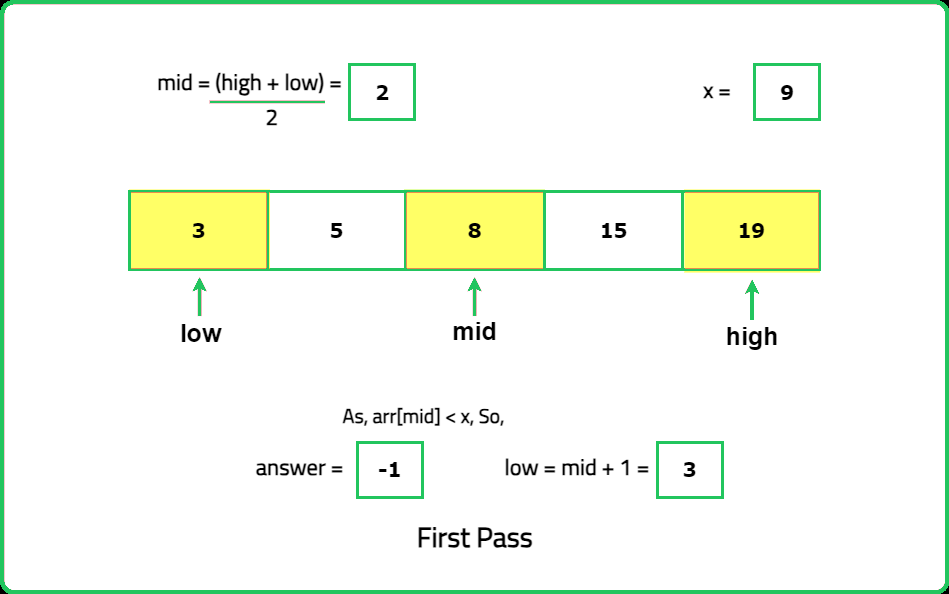
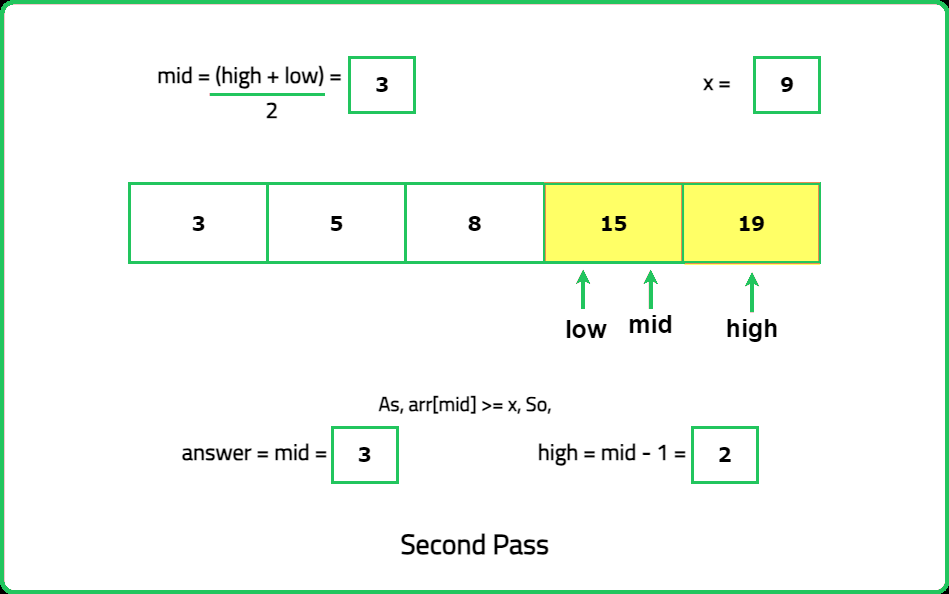
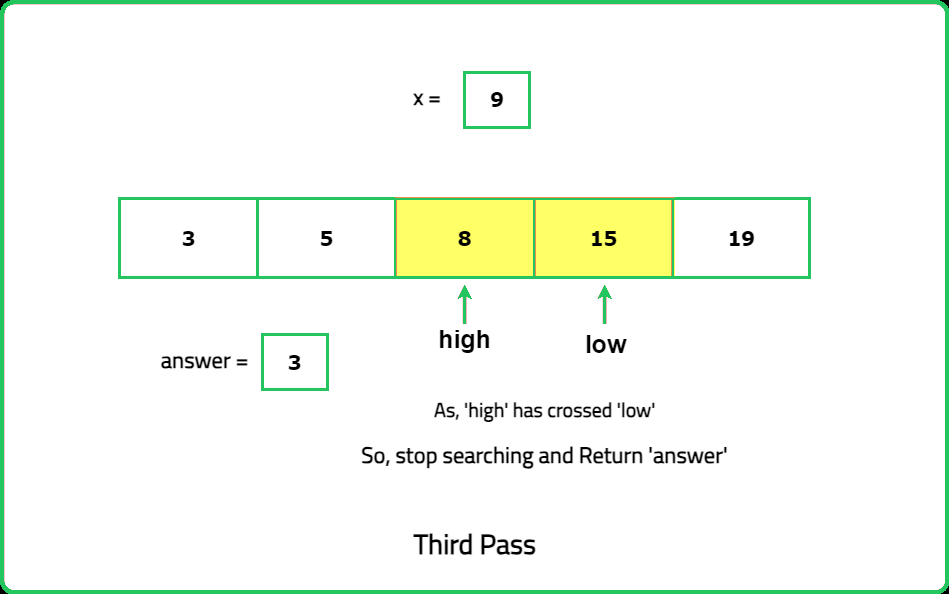
Input : nums= [3,5,8,15,19], x = 9
Output: 3
Explanation: Index 3 is the smallest index such that arr[3] >= x.
Input : nums= [3,5,8,15,19], x = 3
Constraints
- 1 <= nums.length <= 105
- -105 < nums[i], x < 105
- nums is sorted in ascending order.
Hints
- It’s not just about finding x; you’re looking for the first index where the array value is greater than or equal to x.Think of it as finding where x "fits" in the array while maintaining the sorted order.
- "Use binary search logic but modify the condition for moving the pointers. If nums[mid]≥x, the answer might lie to the left, so move the high pointer. Otherwise, move the low pointer to search the right half."
Company Tags
Morgan Stanley
Western Digital
Qualcomm
Broadcom
Ubisoft
ARM
Etsy
Instacart
Lyft
Chewy
GE Healthcare
Siemens Healthineers
Docker
HashiCorp
JPMorgan Chase
Epic Games
Twilio
Robinhood
Teladoc Health
Optum
Swiggy
Salesforce
Target
Goldman Sachs
AMD
TCS
Cognizant
Accenture
Infosys
Capgemini
Wipro