Minimum days to make M bouquets
Binary Search
On answers
Medium
- This problem, at its essence, involves optimal scheduling and resource allocation - concepts critical to many areas in software development
- An interesting real-world application is found in distributed computing or microservices architecture, where you need to manage the execution time and ordering of numerous independent tasks (roses blooming) to meet certain requirements (making bouquets)
- Similarly, this problem can reflect challenges in project management software, where tasks have specific start times (bloom days), and certain tasks have to be completed together (bouquet making) within specified time frames
Given n roses and an array nums where nums[i] denotes that the 'ith' rose will bloom on the nums[i]th day, only adjacent bloomed roses can be picked to make a bouquet. Exactly k adjacent bloomed roses are required to make a single bouquet. Find the minimum number of days required to make at least m bouquets, each containing k roses. Return -1 if it is not possible.
Examples:
Input: n = 8, nums = [7, 7, 7, 7, 13, 11, 12, 7], m = 2, k = 3
Output: 12
Explanation: On the 12th the first 4 flowers and the last 3 flowers would have already bloomed. So, we can easily make 2 bouquets, one with the first 3 and another with the last 3 flowers.
Input: n = 5, nums = [1, 10, 3, 10, 2], m = 3, k = 2
Output: -1
Explanation: If we want to make 3 bouquets of 2 flowers each, we need at least 6 flowers. But we are given only 5 flowers, so, we cannot make the bouquets.
Input: n = 5, nums = [1, 10, 3, 10, 2], m = 3, k = 1
Constraints
- 1 <= n <= 105
- 1 <= nums[i] <= 109
- 1 <= m <= 106
- 1 <= k <= n
Hints
- "Use binary search to determine the smallest d within the range [1,max(nums)]. For each mid-point d, simulate the blooming process to check if at least m bouquets can be formed."
- On a given day d, a rose is considered bloomed if nums[i]≤d. Traverse the array and count adjacent bloomed roses. If k adjacent roses are found, form one bouquet and reset the count. Repeat until m bouquets are formed or the array is exhausted.
Company Tags
Deloitte
Johnson & Johnson
Wayfair
Walmart
Medtronic
Epic Games
Siemens Healthineers
Twilio
Robinhood
Rakuten
Intel
Philips Healthcare
Flipkart
Chewy
Lyft
Micron Technology
Zomato
Roblox
Optum
Qualcomm
GE Healthcare
DoorDash
Zoho
eBay
OYO Rooms
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition:
The very straightforward approach is to check all possible answers from range min to max linearly, where, min is the minimum element of the array and max is the maximum element of the array. Each number in the range shows the number of days. The minimum number of days for which at least 'm' bouquet can be made each containing 'k' rose will be our final answer.
Approach:
Edge case: If the product k*m(minimum number of roses required) is greater than size of the array, then it is impossible to make bouquet, in that case return -1
Working of roseGarden(n, nums, k, m):- Calculate
valas the product of 'm' (number of bouquets) and 'k'( number of roses each bouquet should have), ensuring it's cast to long long to avoid overflow. Determine the size n of the array. - Initialize
miniandmaxito INT_MAX and INT_MIN, respectively, to find the first day when a flower blooms and the last on which all fowers should have already bloomed. - Iterate through the days starting from mini to maxi. For each day , use the possible function to check if the total number of bouquets on this day, each containing k roses is greater than or equal to 'k'. If yes, return the current day as an answer.
- After coming out of the loop, return -1 as no day is found matching the constraints.
Working of possible(nums, day, k):
- First, initialize 'n' is to the size of nums, which represents the number of flowers. Initialize 'cnt' to 0 which keeps track of how many flowers have bloomed within the current day threshold day. Initialize 'noOfB' of 0, keeps track of the total number of bouquets formed.
- The function iterates through each flower's blooming day in nums. For each flower, if its blooming day is less than or equal to day, increment 'cnt' (indicating a flower that can be used to form a bouquet). If a flower's blooming day exceeds day, calculate how many complete bouquets (cnt / k) can be formed with the flowers that bloomed up to that point (cnt). Add this count to noOfB. Reset 'cnt' to zero because flowers blooming after day cannot be used for the current bouquet.
- After iterating through all flowers, there might be remaining flowers (cnt) that have bloomed within day. Calculate how many additional bouquets can be formed with these remaining flowers and add this to noOfB.
- Finally, check if the total number of bouquets (noOfB) formed is greater than or equal to m. If so, return true, indicating that it's possible to form at least m bouquets with the given constraints (day and k).If not, return false.
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192939495
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to check if it's possible to make
m bouquets with k flowers each on day */
bool possible(vector<int> &nums, int day, int m, int k) {
int n = nums.size();
// Count of flowers bloomed
int cnt = 0;
// Count of bouquets formed
int noOfB = 0;
// Count number of bouquets that can be formed
for (int i = 0; i < n; i++) {
if (nums[i] <= day) {
// Increment flower count
cnt++;
} else {
/* Calculate number of bouquets
formed with flowers <= day */
noOfB += (cnt / k);
// Reset flower count
cnt = 0;
}
}
// Add remaining flowers as a bouquet
noOfB += (cnt / k);
/* Return true if enough
bouquets can be formed */
return noOfB >= m;
}
public:
/* Function to find the earliest day to
make m bouquets of k flowers each */
int roseGarden(int n, vector<int> nums, int k, int m) {
/* Calculate the minimum
number of flowers required*/
long long val = m * 1ll * k * 1ll;
/* Impossible case: not enough
flowers to make m bouquets*/
if (val > n) return -1;
/* Find maximum and minimum
bloom days in the array */
int mini = INT_MAX, maxi = INT_MIN;
for (int i = 0; i < n; i++) {
mini = min(mini, nums[i]);
maxi = max(maxi, nums[i]);
}
/* Linear search to find the
earliest day to make m bouquets */
for (int i = mini; i <= maxi; i++) {
if (possible(nums, i, m, k))
return i;
}
// Return-1 if no such day exists
return -1;
}
};
int main() {
vector<int> arr = {7, 7, 7, 7, 13, 11, 12, 7};
int n = arr.size();
// Number of flowers per bouquet
int k = 3;
// Number of bouquets needed
int m = 2;
// Create an instance of the Solution class
Solution sol;
int ans = sol.roseGarden(n, arr, k, m);
if (ans == -1) {
cout << "We cannot make m bouquets.\n";
} else {
cout << "We can make bouquets on day " << ans << "\n";
}
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182838485868788899091
import java.util.*;
class Solution {
/* Function to check if it's possible to make
m bouquets with k flowers each on day*/
private boolean possible(int[] nums, int day, int m, int k) {
int n = nums.length;
// Count of flowers bloomed
int cnt = 0;
// Count of bouquets formed
int noOfB = 0;
// Count number of bouquets that can be formed
for (int i = 0; i < n; i++) {
if (nums[i] <= day) {
// Increment flower count
cnt++;
} else {
/* Calculate number of bouquets
formed with flowers <= day */
noOfB += (cnt / k);
// Reset flower count
cnt = 0;
}
}
// Add remaining flowers as a bouquet
noOfB += (cnt / k);
/* Return true if enough
bouquets can be formed */
return noOfB >= m;
}
/* Function to find the earliest day to
make m bouquets of k flowers each*/
public int roseGarden(int n, int[] nums, int k, int m) {
/* Calculate the minimum
number of flowers required*/
long val = (long) m * k;
/* Impossible case: not enough
flowers to make m bouquets*/
if (val > n) return -1;
/* Find maximum and minimum
bloom days in the array */
int mini = Integer.MAX_VALUE, maxi = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
mini = Math.min(mini, nums[i]);
maxi = Math.max(maxi, nums[i]);
}
/* Linear search to find the
earliest day to make m bouquets */
for (int i = mini; i <= maxi; i++) {
if (possible(nums, i, m, k))
return i;
}
// Return-1 if no such day exists
return -1;
}
public static void main(String[] args) {
int[] arr = {7, 7, 7, 7, 13, 11, 12, 7};
int n = arr.length;
// Number of flowers per bouquet
int k = 3;
// Number of bouquets needed
int m = 2;
// Create an instance of the Solution class
Solution sol = new Solution();
int ans = sol.roseGarden(n, arr, k, m);
if (ans == -1) {
System.out.println("We cannot make m bouquets.");
} else {
System.out.println("We can make bouquets on day " + ans);
}
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667686970717273747576777879808182
class Solution:
"""Function to check if it's possible to make
m bouquets with k flowers each on a given day"""
def possible(self, nums, day, m, k):
n = len(nums)
# Count of flowers bloomed
cnt = 0
# Count of bouquets formed
noOfB = 0
# Count number of bouquets that can be formed
for i in range(n):
if nums[i] <= day:
# Increment flower count
cnt += 1
else:
# Calculate number of bouquets formed with flowers <= day
noOfB += (cnt // k)
# Reset flower count
cnt = 0
# Add remaining flowers as a bouquet
noOfB += (cnt // k)
# Return true if enough bouquets can be formed
return noOfB >= m
"""Function to find the earliest day to
make m bouquets of k flowers each"""
def roseGarden(self, n, nums, k, m):
# Calculate the minimum number of flowers required
val = m * k
# Impossible case: not enough flowers to make m bouquets
if val > n:
return -1
# Find maximum and minimum bloom days in the array
mini = float('inf')
maxi = float('-inf')
for num in nums:
mini = min(mini, num)
maxi = max(maxi, num)
# Linear search to find the earliest day to make m bouquets
for i in range(mini, maxi + 1):
if self.possible(nums, i, m, k):
return i
# Return -1 if no such day exists
return -1
if __name__ == "__main__":
arr = [7, 7, 7, 7, 13, 11, 12, 7]
n = len(arr)
# Number of flowers per bouquet
k = 3
# Number of bouquets needed
m = 2
# Create an instance of the Solution class
sol = Solution()
ans = sol.roseGarden(n, arr, k, m)
if ans == -1:
print("We cannot make m bouquets.")
else:
print(f"We can make bouquets on day {ans}")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889
class Solution {
/* Function to check if it's possible to make
m bouquets with k flowers each on day */
possible(nums, day, m, k) {
let n = nums.length;
// Count of flowers bloomed
let cnt = 0;
// Count of bouquets formed
let noOfB = 0;
// Count number of bouquets that can be formed
for (let i = 0; i < n; i++) {
if (nums[i] <= day) {
// Increment flower count
cnt++;
} else {
/* Calculate number of bouquets
formed with flowers <= day */
noOfB += Math.floor(cnt / k);
// Reset flower count
cnt = 0;
}
}
// Add remaining flowers as a bouquet
noOfB += Math.floor(cnt / k);
/* Return true if enough
bouquets can be formed */
return noOfB >= m;
}
/* Function to find the earliest day to
make m bouquets of k flowers each */
roseGarden(n, nums, k, m) {
/* Calculate the minimum
number of flowers required */
let val = m * k;
/* Impossible case: not enough
flowers to make m bouquets */
if (val > n) return -1;
/* Find maximum and minimum
bloom days in the array */
let mini = Infinity, maxi = -Infinity;
for (let i = 0; i < n; i++) {
mini = Math.min(mini, nums[i]);
maxi = Math.max(maxi, nums[i]);
}
/* Linear search to find the
earliest day to make m bouquets */
for (let i = mini; i <= maxi; i++) {
if (this.possible(nums, i, m, k)) {
return i;
}
}
// Return -1 if no such day exists
return -1;
}
}
function main() {
let arr = [7, 7, 7, 7, 13, 11, 12, 7];
let n = arr.length;
// Number of flowers per bouquet
let k = 3;
// Number of bouquets needed
let m = 2;
// Create an instance of the Solution class
let sol = new Solution();
let ans = sol.roseGarden(n, arr, k, m);
if (ans == -1) {
console.log("We cannot make m bouquets.");
} else {
console.log("We can make bouquets on day " + ans);
}
}
main();
Complexity Analysis:
Time Complexity:O((max-min+1) * N), where max is the maximum element of the array, min is the minimum element of the array, N is size of the array}.Space Complexity: As no additional space is used, so the Space Complexity is O(1).
Intuition:
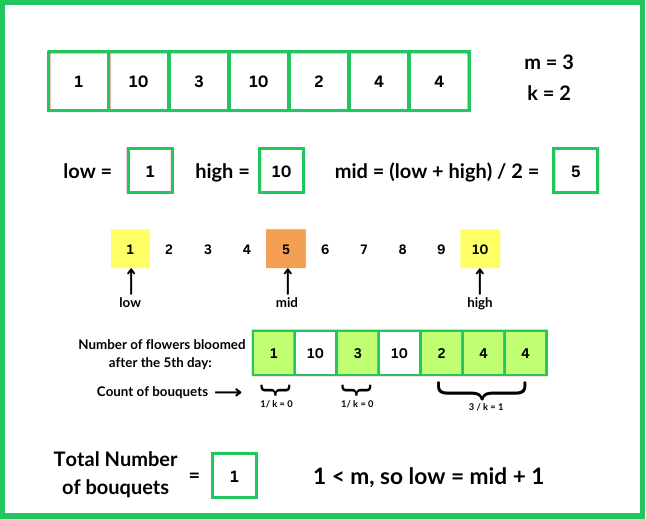
The idea here is to use binary search algorithm as the search range[min, max] is sorted, where, min is the earliest and max is the latest day for a rose to bloom. So, if it's feasible to make m bouquets on day 'mid'((low+high)/2), eliminate the right half of the search space to search for an earlier day. Else, eliminate the left half to find a higher range of days. This way, the brute-force solution can be optimized.
Approach:
Edge case: If the product k*m is greater than size of the array, then it is impossible to make bouquet, in that case return -1.
Working of roseGarden(n, nums, k, m):- Initialize
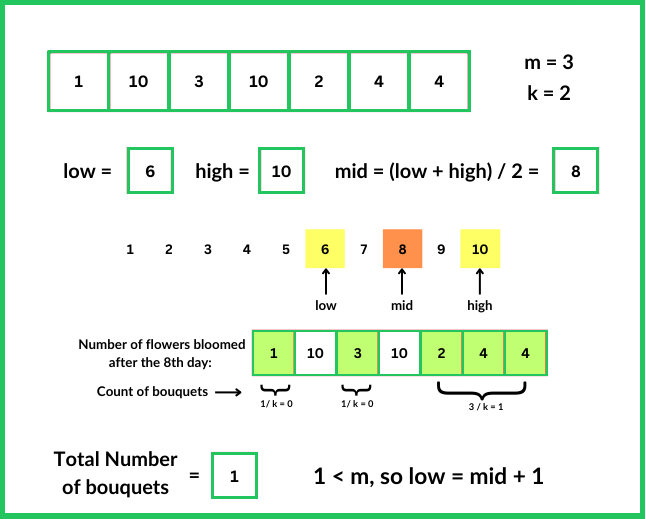
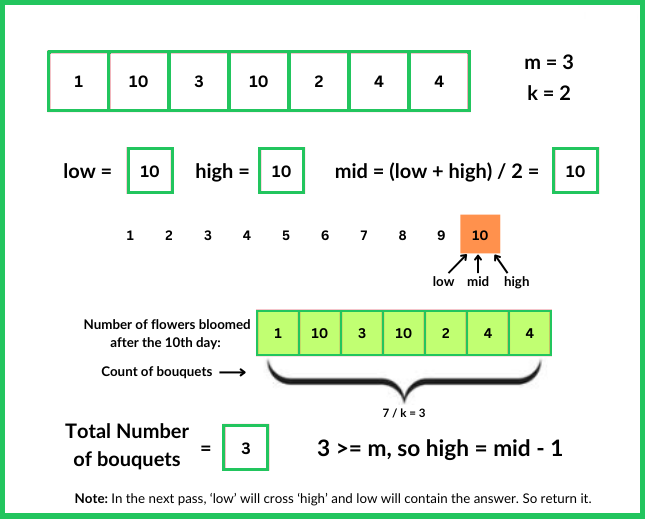
minito INT_MAX andmaxito INT_MIN to find the earliest and latest bloom days in the nums array. - Use binary search to find the earliest day (ans) where it’s possible to make m bouquets of k flowers each. Initialize left to mini and right to maxi. The range [low,high] defines the search space.
- While left is less than or equal to right, calculate the middle day 'mid'. Use the possible function to check if it's feasible to make m bouquets on day mid. If feasible, update ans to mid and move right to mid - 1 to search for an earlier day. Otherwise, move left to mid + 1 to search in the higher range of days.
- After the binary search completes, ans will hold the earliest day on which it's possible to make m bouquets of k flowers each. Return ans. If no such day exists (ans remains -1), return -1 indicating it's not possible under the given constraints.
Working of possible(nums, day, k):
- First, initialize 'n' is to the size of nums, which represents the number of flowers. Initialize 'cnt' to 0 which keeps track of how many flowers have bloomed within the current day threshold day. Initialize 'noOfB' of 0, keeps track of the total number of bouquets formed.
- The function iterates through each flower's blooming day in nums. For each flower, if its blooming day is less than or equal to day, increment 'cnt' (indicating a flower that can be used to form a bouquet). If a flower's blooming day exceeds day, calculate how many complete bouquets (cnt / k) can be formed with the flowers that bloomed up to that point (cnt). Add this count to noOfB. Reset 'cnt' to zero because flowers blooming after day cannot be used for the current bouquet.
- After iterating through all flowers, there might be remaining flowers (cnt) that have bloomed within day. Calculate how many additional bouquets can be formed with these remaining flowers and add this to noOfB.
- Finally, check if the total number of bouquets (noOfB) formed is greater than or equal to m. If so, return true, indicating that it's possible to form at least m bouquets with the given constraints (day and k).If not, return false.
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to check if it's possible to make
m bouquets with k flowers each on day */
bool possible(vector<int> &nums, int day, int m, int k) {
int n = nums.size();
// Count of flowers bloomed
int cnt = 0;
// Count of bouquets formed
int noOfB = 0;
// Count number of bouquets that can be formed
for (int i = 0; i < n; i++) {
if (nums[i] <= day) {
// Increment flower count
cnt++;
} else {
/* Calculate number of bouquets
formed with flowers <= day */
noOfB += (cnt / k);
// Reset flower count
cnt = 0;
}
}
// Add remaining flowers as a bouquet
noOfB += (cnt / k);
/* Return true if enough
bouquets can be formed */
return noOfB >= m;
}
public:
/* Function to find the earliest day to
make m bouquets of k flowers each */
int roseGarden(int n, vector<int> nums, int k, int m) {
/* Calculate the minimum
number of flowers required*/
long long val = m * 1ll * k * 1ll;
/* Impossible case: not enough
flowers to make m bouquets*/
if (val > n) return -1;
/* Find maximum and minimum
bloom days in the array */
int mini = INT_MAX, maxi = INT_MIN;
for (int i = 0; i < n; i++) {
mini = min(mini, nums[i]);
maxi = max(maxi, nums[i]);
}
/* Binary search to find the
earliest day to make m bouquets */
int left = mini, right = maxi, ans = -1;
while (left <= right) {
// Calculate the middle day
int mid = left + (right - left) / 2;
/* Check if it's possible to
make m bouquets on day mid */
if (possible(nums, mid, m, k)) {
// Update the answer to mid
ans = mid;
// Try for a smaller day
right = mid - 1;
} else {
left = mid + 1;
}
}
/* Return the earliest day or
-1 if no such day exists */
return ans;
}
};
int main() {
vector<int> arr = {7, 7, 7, 7, 13, 11, 12, 7};
int n = arr.size();
// Number of flowers per bouquet
int k = 3;
// Number of bouquets needed
int m = 2;
// Create an instance of the Solution class
Solution sol;
int ans = sol.roseGarden(n, arr, k, m);
if (ans == -1) {
cout << "We cannot make m bouquets.\n";
} else {
cout << "We can make bouquets on day " << ans << "\n";
}
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107
import java.util.*;
class Solution {
/* Function to check if it's possible to make
m bouquets with k flowers each on day*/
private boolean possible(int[] nums, int day, int m, int k) {
int n = nums.length;
// Count of flowers bloomed
int cnt = 0;
// Count of bouquets formed
int noOfB = 0;
// Count number of bouquets that can be formed
for (int i = 0; i < n; i++) {
if (nums[i] <= day) {
// Increment flower count
cnt++;
} else {
/* Calculate number of bouquets
formed with flowers <= day */
noOfB += (cnt / k);
// Reset flower count
cnt = 0;
}
}
// Add remaining flowers as a bouquet
noOfB += (cnt / k);
/* Return true if enough
bouquets can be formed */
return noOfB >= m;
}
/* Function to find the earliest day to
make m bouquets of k flowers each*/
public int roseGarden(int n, int[] nums, int k, int m) {
/* Calculate the minimum
number of flowers required*/
long val = (long) m * k;
/* Impossible case: not enough
flowers to make m bouquets*/
if (val > n) return -1;
/* Find maximum and minimum
bloom days in the array */
int mini = Integer.MAX_VALUE, maxi = Integer.MIN_VALUE;
for (int i = 0; i < n; i++) {
mini = Math.min(mini, nums[i]);
maxi = Math.max(maxi, nums[i]);
}
/* Binary search to find the
earliest day to make m bouquets */
int left = mini, right = maxi, ans = -1;
while (left <= right) {
// Calculate the middle day
int mid = left + (right - left) / 2;
/* Check if it's possible to
make m bouquets on day mid */
if (possible(nums, mid, m, k)) {
// Update the answer to mid
ans = mid;
// Try for a smaller day
right = mid - 1;
} else {
left = mid + 1;
}
}
/* Return the earliest day or
-1 if no such day exists*/
return ans;
}
public static void main(String[] args) {
int[] arr = {7, 7, 7, 7, 13, 11, 12, 7};
int n = arr.length;
// Number of flowers per bouquet
int k = 3;
// Number of bouquets needed
int m = 2;
// Create an instance of the Solution class
Solution sol = new Solution();
int ans = sol.roseGarden(n, arr, k, m);
if (ans == -1) {
System.out.println("We cannot make m bouquets.");
} else {
System.out.println("We can make bouquets on day " + ans);
}
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100
class Solution:
"""Function to check if it's possible to make
m bouquets with k flowers each on day """
def possible(self, nums, day, m, k):
n = len(nums)
# Count of flowers bloomed
cnt = 0
# Count of bouquets formed
noOfB = 0
# Count number of bouquets that can be formed
for i in range(n):
if nums[i] <= day:
# Increment flower count
cnt += 1
else:
""" Calculate number of bouquets
formed with flowers <= day """
noOfB += (cnt // k)
# Reset flower count
cnt = 0
# Add remaining flowers as a bouquet
noOfB += (cnt // k)
""" Return true if enough
bouquets can be formed """
return noOfB >= m
""" Function to find the earliest day to
make m bouquets of k flowers each """
def roseGarden(self, n, nums, k, m):
""" Calculate the minimum
number of flowers required """
val = m * k
""" Impossible case: not enough
flowers to make m bouquets """
if val > n:
return -1
""" Find maximum and minimum
bloom days in the array """
mini = float('inf')
maxi = float('-inf')
for num in nums:
mini = min(mini, num)
maxi = max(maxi, num)
""" Binary search to find the
earliest day to make m bouquets """
left = mini
right = maxi
ans = -1
while left <= right:
# Calculate the middle day
mid = left + (right - left) // 2
""" Check if it's possible to
make m bouquets on day mid """
if self.possible(nums, mid, m, k):
# Update the answer to mid
ans = mid
# Try for a smaller day
right = mid - 1
else:
left = mid + 1
""" Return the earliest day or
-1 if no such day exists"""
return ans
if __name__ == "__main__":
arr = [7, 7, 7, 7, 13, 11, 12, 7]
n = len(arr)
# Number of flowers per bouquet
k = 3
# Number of bouquets needed
m = 2
# Create an instance of the Solution class
sol = Solution()
ans = sol.roseGarden(n, arr, k, m)
if ans == -1:
print("We cannot make m bouquets.")
else:
print(f"We can make bouquets on day {ans}")
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105
class Solution {
/* Function to check if it's possible to make
m bouquets with k flowers each on day */
possible(nums, day, m, k) {
let n = nums.length;
// Count of flowers bloomed
let cnt = 0;
// Count of bouquets formed
let noOfB = 0;
// Count number of bouquets that can be formed
for (let i = 0; i < n; i++) {
if (nums[i] <= day) {
// Increment flower count
cnt++;
} else {
/* Calculate number of bouquets
formed with flowers <= day */
noOfB += Math.floor(cnt / k);
// Reset flower count
cnt = 0;
}
}
// Add remaining flowers as a bouquet
noOfB += Math.floor(cnt / k);
/* Return true if enough
bouquets can be formed */
return noOfB >= m;
}
/*Function to find the earliest day to
make m bouquets of k flowers each */
roseGarden(n, nums, k, m) {
/* Calculate the minimum
number of flowers required */
let val = m * k;
/* Impossible case: not enough
flowers to make m bouquets */
if (val > n) return -1;
/* Find maximum and minimum
bloom days in the array */
let mini = Infinity, maxi = -Infinity;
for (let i = 0; i < n; i++) {
mini = Math.min(mini, nums[i]);
maxi = Math.max(maxi, nums[i]);
}
/* Binary search to find the
earliest day to make m bouquets */
let left = mini, right = maxi, ans = -1;
while (left <= right) {
// Calculate the middle day
let mid = left + Math.floor((right - left) / 2);
/* Check if it's possible to
make m bouquets on day mid */
if (this.possible(nums, mid, m, k)) {
// Update the answer to mid
ans = mid;
// Try for a smaller day
right = mid - 1;
} else {
left = mid + 1;
}
}
/* Return the earliest day or
-1 if no such day exists */
return ans;
}
}
function main() {
let arr = [7, 7, 7, 7, 13, 11, 12, 7];
let n = arr.length;
// Number of flowers per bouquet
let k = 3;
// Number of bouquets needed
let m = 2;
// Create an instance of the Solution class
let sol = new Solution();
let ans = sol.roseGarden(n, arr, k, m);
if (ans == -1) {
console.log("We cannot make m bouquets.");
} else {
console.log("We can make bouquets on day " + ans);
}
}
main();
Complexity Analysis:
Time Complexity:O(log(max-min+1) * N), where max is the maximum element of the array, min is the minimum element of the array, N is size of the array.Space Complexity: As no additional space is used, so the Space Complexity is O(1).
Frequently Occurring Doubts
Q: How is bouquet feasibility checked efficiently?
A: Use a single pass through the array on day d: Count consecutive roses that bloom on or before d. Reset the count whenever nums[i]>d. Stop early if m bouquets are formed, optimizing the simulation.
Q: Why use binary search to find the minimum days?
A: Testing each day from 1 to max(nums) linearly has O(n⋅max(nums)) complexity, which is inefficient. Binary search narrows down the range logarithmically, significantly reducing the number of simulations.
Interview Followup Questions
Q: How would you handle non-adjacent bouquets?
A: For non-adjacent bouquets, modify the simulation to track individual roses that bloom on or before d. Count all such roses and check if their total is sufficient to form m⋅k bouquets.
Q: What if the roses bloom asynchronously, with delays or dependencies?
A: Model blooming as a graph, where edges represent dependencies. Use topological sorting to calculate effective blooming times and then apply the same binary search logic.
Notes
Code
✅ Testcase
Input: {'k': '3', 'm': '2', 'nums': '[7, 7, 7, 7, 13, 11, 12, 7]'}
Expected:
12
12
Actual: -
Time: -
sec
Status: Waiting
Input: {'k': '2', 'm': '3', 'nums': '[1, 10, 3, 10, 2]'}
Expected:
-1
-1
Actual: -
Time: -
sec
Status: Waiting
Input: {'k': '1', 'm': '3', 'nums': '[1, 10, 3, 10, 2]'}
Expected:
3
3
Actual: -
Time: -
sec
Status: Waiting