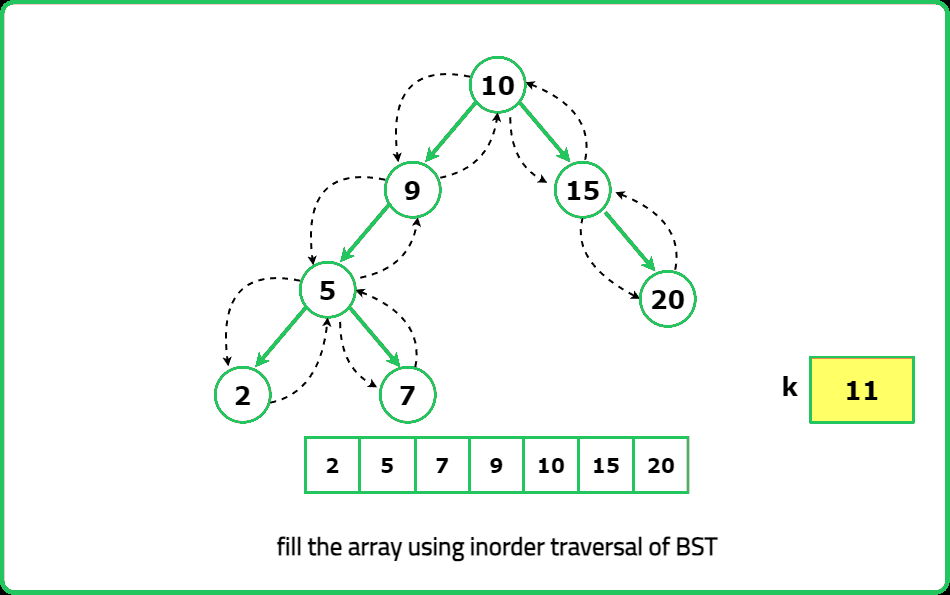
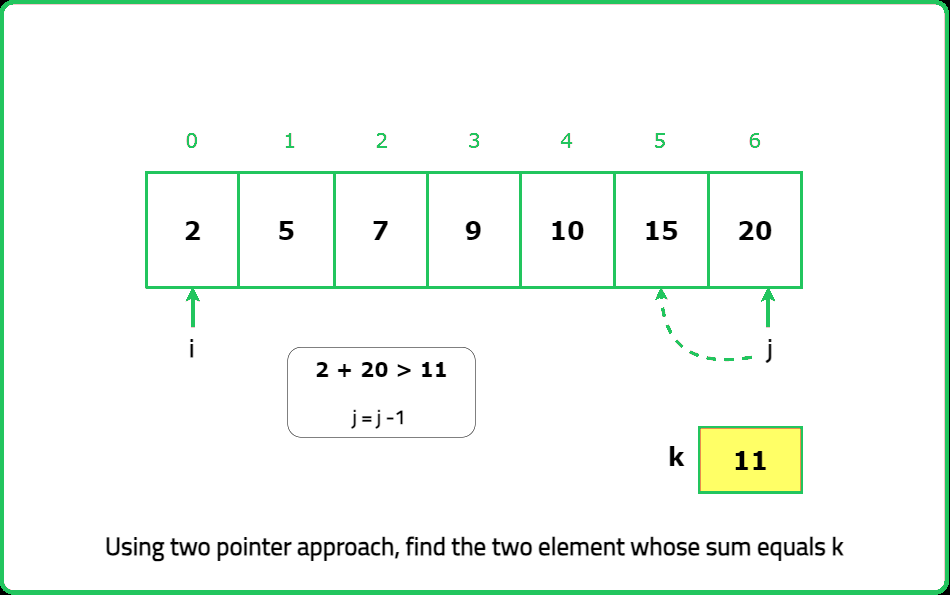
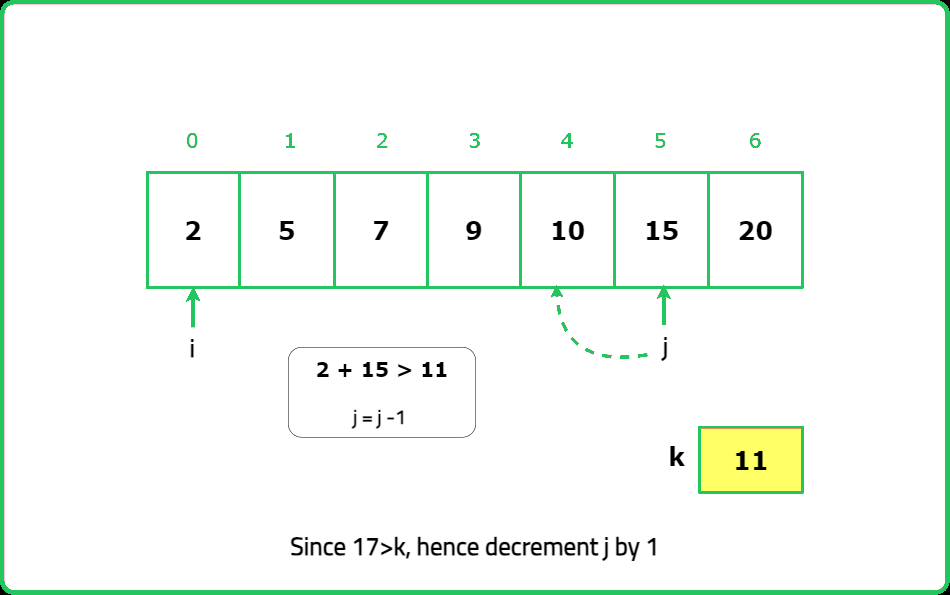
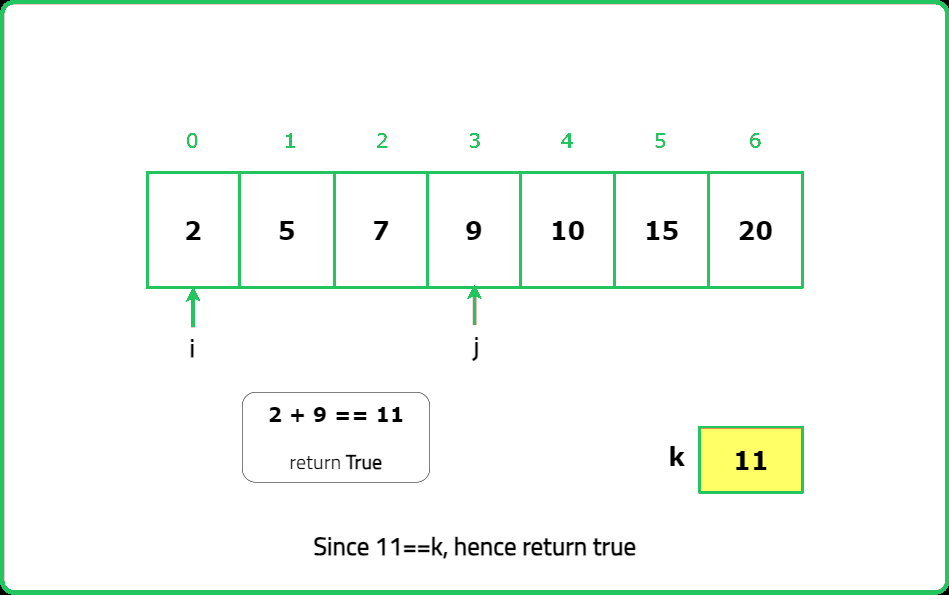
Two sum in BST
Binary Search Trees
FAQs
Hard
- This programming problem is essentially the underpinning of a lot of algorithmic problem-solving and decision-making that goes on in real-time applications
- A fun fact about this problem is that it is actually used in financial trading software
- In these systems, a balance needs to be maintained and therefore, it is often required to find two numbers in a dataset that sum to a certain value
- This helps in maintaining that balance and making sure that the trading activities always net out
- This operation has to be very fast, and binary search trees are one of the most efficient data structures for this purpose
Given the root of a binary search tree and an integer k.Return true if there exist two elements in the BST such that their sum is equal to k otherwise false.
Examples:
Input : root = [5, 3, 6, 2, 4, null, 7] , k = 9
Output : true
Explanation : The BST contains multiple pair of nodes that sum up to k.
3 + 6 => 9.
5 + 4 => 9.
2 + 7 => 9.
Input : root = [5, 3, 6, 2, 4, null, 7] , k = 14
Output : false
Explanation : There is no pair in given BST that sum up to k.
Input : root = [5, 3, 6, 2, 4, null, 7] , k = 12
Constraints
- 1 <= Number of Nodes <= 104
- -104 <= Node.val <= 104
- -105 <= k <= 105
Hints
- "Perform inorder traversal and store elements in a hash set. For each node x, check if k - x exists in the hash set. If found, return True, otherwise continue."
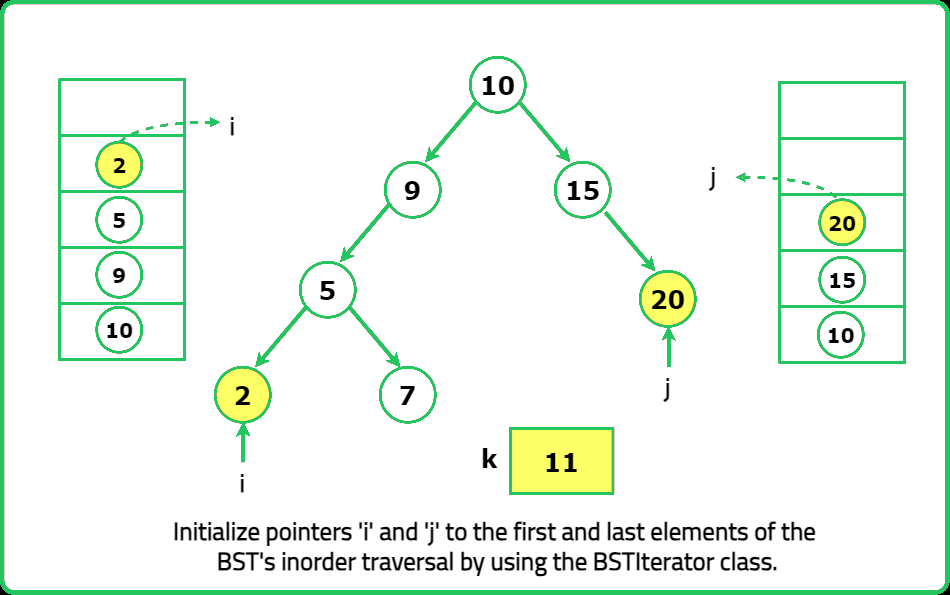
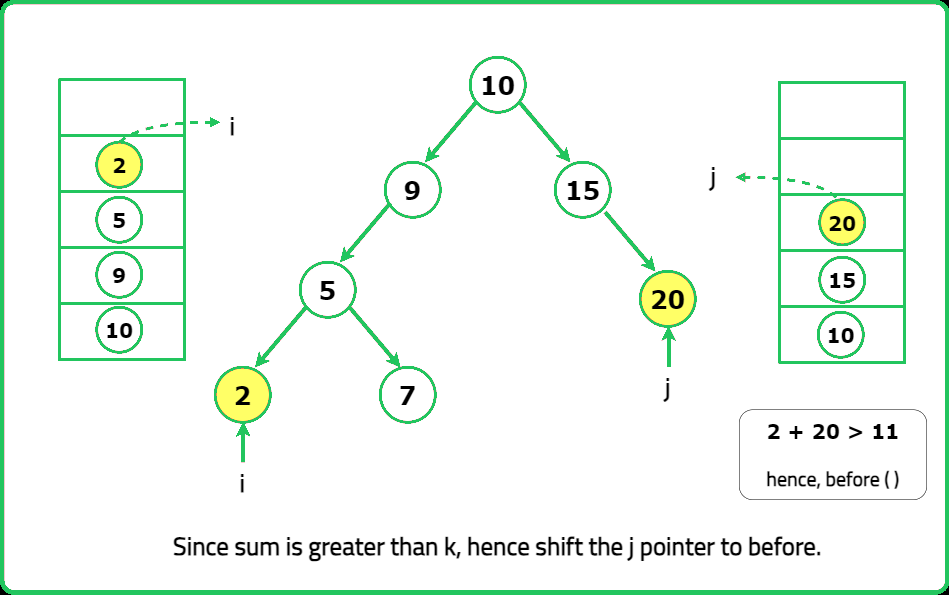
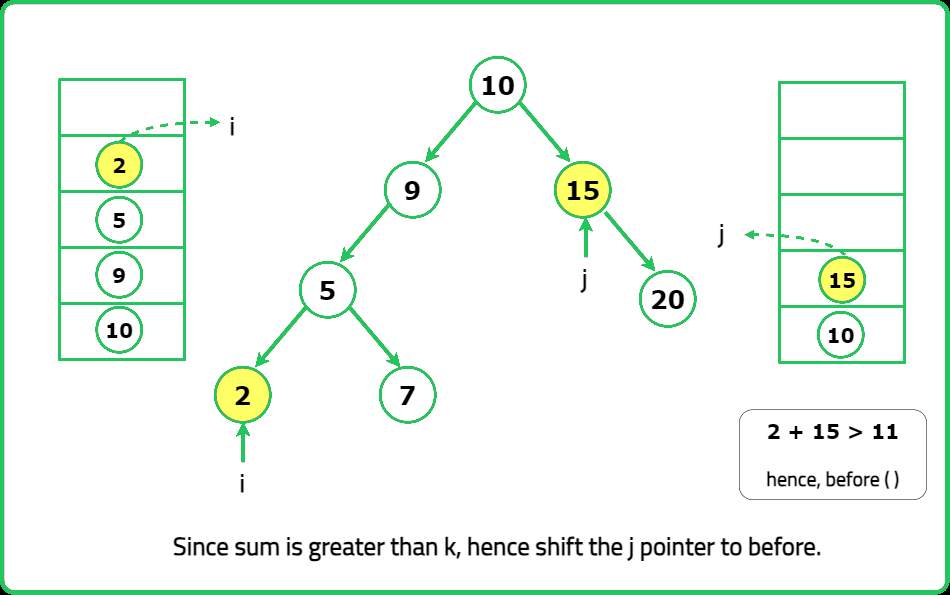
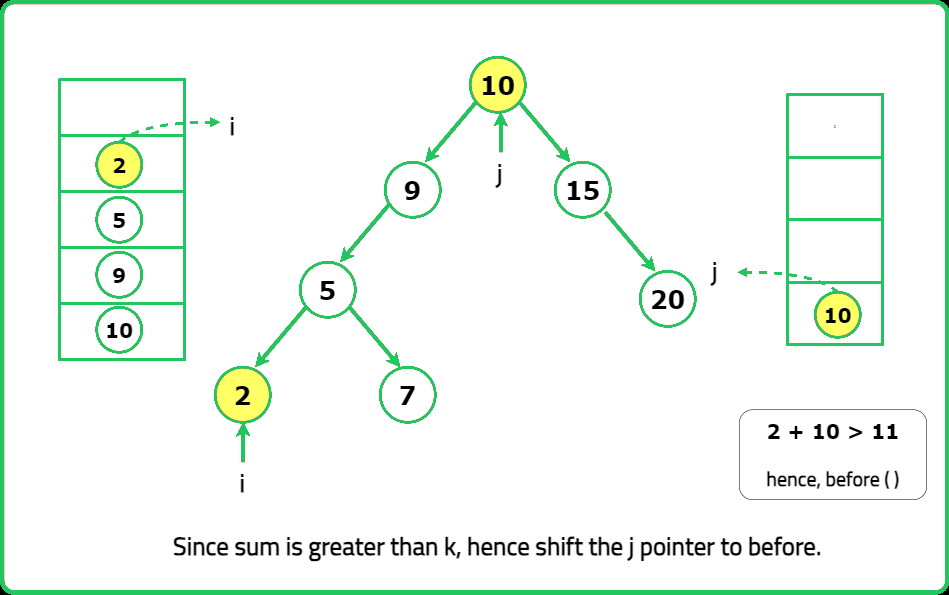
- "Use BST Iterator (next()) for inorder traversal (ascending order). Use Reverse BST Iterator (prev()) for reverse inorder (descending order). Compare smallest + largest using two iterators."
Company Tags
Siemens Healthineers
Unity Technologies
HCL Technologies
Bungie
ARM
Seagate Technology
Freshworks
Rakuten
Cerner
Optum
Intel
Visa
Shopify
Instacart
Square
Medtronic
Bain & Company
Western Digital
KPMG
Salesforce
Johnson & Johnson
Airbnb
Twilio
AMD
Mastercard
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe