Minimum Bit Flips to Convert Number

Bit Manipulation Problems Medium Go Ad-Free - ₹20/mo

Given two integers start and goal. Flip the minimum number of bits of start integer to convert it into goal integer.

A bits flip in the number val is to choose any bit in binary representation of val and flipping it from either 0 to 1 or 1 to 0.

Examples:

Input : start = 10 , goal = 7

Output : 3

Explanation : The binary representation of 10 is "1010".

The binary representation of 7 is "111".

If we flip the underlined bits in binary representation of 10 then we will obtain our goal.

Input : start = 3 , goal = 4

Output : 3

Explanation : The binary representation of 3 is "011".

The binary representation of 4 is "100".

So if we flip all the three bits of 3 then we will reach our goal number.

Input : start = 1 , goal = 7

Constraints

1 <= start , end <= 10⁹

Hints

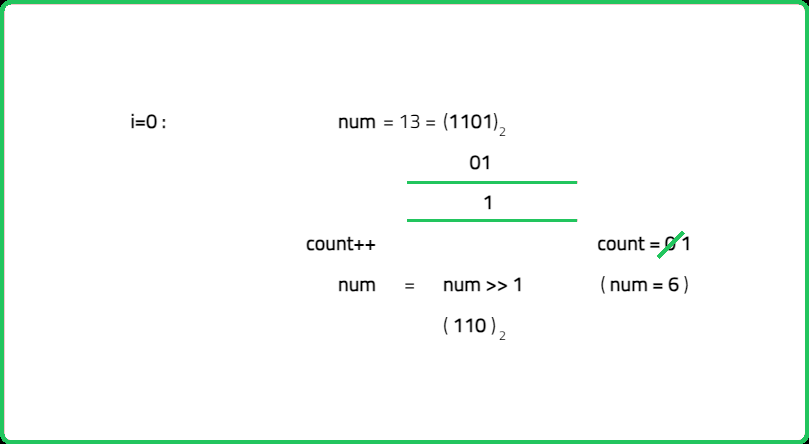
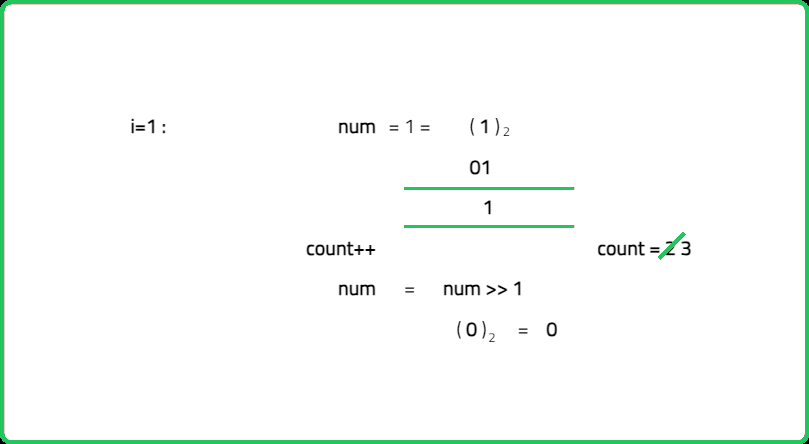
To convert start to goal, XOR the two integers. The result of XOR will have 1s at all the bit positions where start and goal differ.
"Count the number of 1s in the XOR result. Each 1 corresponds to a bit that needs to be flipped to convert start into goal. This count gives the minimum number of bit flips required. "

Company Tags

Reddit Ernst & Young Flipkart American Express Byju's Morgan Stanley Walmart Airbnb Optum Databricks Swiggy Roche DoorDash IBM HCL Technologies Stripe NVIDIA Johnson & Johnson Zomato ARM McKinsey & Company Twilio Boston Consulting Group MongoDB Electronic Arts Google Microsoft Amazon Meta Apple Netflix Adobe

Editorial

Intuition

Since the problem is asking about number of bits that needs to be changed, it could be easily find out if it is known that which are bits are different.
And for this purpose, XOR operation will come in hand which will only set the bit if both corresponding bits are different.

Approach

Use the XOR operation between the two numbers. This will produce a new number where each bit is set to 1 if the corresponding bits in the original numbers were different.
Count the number of 1s in this new number because each 1 represents a bit that needs to be flipped to convert one number to the other.
Run a loop 32 times (to check all 32 bits in the number) and shift the bits of this new number one by one. Check if the least significant bit (the rightmost bit) is 1. If it is, increment the count.
Repeat this shifting process until all bits in the number have been checked. The count will give the minimum number of bit flips required to convert the first number into the second.

Dry Run:

Solution:

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to get the minimum
     bit flips to convert number */
    int minBitsFlip(int start, int goal) {
        
        /* Variable to store bits that
        are different in both numbers */
        int num = start ^ goal;
        
        /* Variable to count 
        number of set bits */
        int count = 0;

        for(int i = 0; i < 32; i++) {
            /* Update count if the 
            rightmost bit is set */
            count += (num & 1); 
            
            /* Shift the number every 
            time by 1 place */
            num = num >> 1;
        }
        return count;
    }
};

int main() {
    int start = 10, goal = 7;
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to get the minimum
     bit flips to convert number */
    int ans = sol.minBitsFlip(start, goal);
    
    cout << "The minimum bit flips to convert number is: " << ans;
    
    return 0;
}
 class Solution {
    /* Function to get the minimum
     bit flips to convert number */
    public int minBitsFlip(int start, int goal) {
        
        /* Variable to store bits that
        are different in both numbers */
        int num = start ^ goal;
        
        /* Variable to count 
        number of set bits */
        int count = 0;

        for (int i = 0; i < 32; i++) {
            /* Update count if the 
            rightmost bit is set */
            count += (num & 1); 
            
            /* Shift the number every 
            time by 1 place */
            num = num >> 1;
        }
        return count;
    }

    public static void main(String[] args) {
        int start = 10, goal = 7;
        
        /* Creating an instance of 
        Solution class */
        Solution sol = new Solution(); 
        
        /* Function call to get the minimum
         bit flips to convert number */
        int ans = sol.minBitsFlip(start, goal);
        
        System.out.println("The minimum bit flips to convert number is: " + ans);
    }
}
class Solution:
    # Function to get the minimum 
    # bit flips to convert number
    def minBitsFlip(self, start, goal):
        
        # Variable to store bits that 
        # are different in both numbers
        num = start ^ goal
        
        # Variable to count 
        # number of set bits
        count = 0

        for i in range(32):
            # Update count if the 
            # rightmost bit is set
            count += (num & 1)
            
            # Shift the number every
            # time by 1 place
            num = num >> 1
        
        return count

# Main function
if __name__ == "__main__":
    start, goal = 10, 7
    
    # Creating an instance of Solution class
    sol = Solution()
    
    # Function call to get the minimum 
    # bit flips to convert number
    ans = sol.minBitsFlip(start, goal)
    
    print("The minimum bit flips to convert number is:", ans)
class Solution {
    /* Function to get the minimum
     bit flips to convert number */
    minBitsFlip(start, goal) {
        
        /* Variable to store bits that
        are different in both numbers */
        let num = start ^ goal;
        
        /* Variable to count 
        number of set bits */
        let count = 0;

        for (let i = 0; i < 32; i++) {
            /* Update count if the 
            rightmost bit is set */
            count += (num & 1);
            
            /* Shift the number every 
            time by 1 place */
            num = num >> 1;
        }
        return count;
    }
}

// Main function
const start = 10, goal = 7;

/* Creating an instance of 
Solution class */
const sol = new Solution();

/* Function call to get the minimum
 bit flips to convert number */
const ans = sol.minBitsFlip(start, goal);

console.log("The minimum bit flips to convert number is:", ans);

Complexity Analysis:

Time Complexity: O(1)

The XOR operation between two integers is performed in constant time, O(1).

The for loop iterates over a fixed number of bits (32 bits for a standard integer), which is as good as O(1).

Space Complexity: O(1) – Using a couple of variables i.e., constant space.

Frequently Occurring Doubts

Q: What is the purpose of XOR in this problem?

A: XOR is used because it directly identifies the bits that differ between two numbers. A 1 in the XOR result means the corresponding bit in start and goal is different.

Q: Does the position of bits affect the solution?

A: No, only the count of differing bits matters. The problem doesn’t require reordering bits, just flipping them where they differ.

Interview Followup Questions

Q: What is the significance of XOR in bit manipulation tasks?

A: XOR is a powerful tool for detecting differences between two binary numbers. It has applications in checksum calculations, encryption, and toggling bits efficiently.

Q: How would you extend this to find the positions of the flipped bits?

A: You can loop through the binary representation of the XOR result and note the indices of 1s. Each 1 corresponds to a flipped bit position.

Notes

Your notes are automatically saved in your browser's local storage and will persist across sessions on this device.

Problem Categories