123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109
#include <bits/stdc++.h>
using namespace std;
/* Define P as a shorthand for
the pair<long long,int> type */
#define P pair<long long,int>
class Solution {
public:
/* Function to get the number of ways to arrive
at destinations in shortest possible time */
int countPaths(int n, vector<vector<int>>& roads) {
int mod = 1e9 + 7; // Mod value
// To store the graph
vector<pair<int,int>> adj[n];
// Adding the edges to the graph
for(auto it : roads) {
adj[it[0]].push_back({it[1] , it[2]});
adj[it[1]].push_back({it[0] , it[2]});
}
/* Array to store the minimum
time to get to nodes */
vector<long long> minTime(n, LLONG_MAX);
/* To store the number of
ways to reach nodes */
vector<int> ways(n, 0);
// Priority queue to store: {time, node}
priority_queue <P, vector<P>, greater<P>> pq;
//Initial configuration
minTime[0] = 0;
ways[0] = 1;
pq.push({0, 0});
// Until the priority queue is empty
while(!pq.empty()) {
// Get the element
auto p = pq.top();
pq.pop();
long long time = p.first; // time
int node = p.second; // node
// Traverse its neighbors
for(auto it : adj[node]) {
int adjNode = it.first; // adjacent node
int travelTime = it.second; // travel time
/* If the current time taken is less than
earlier known time to reach adjacent node */
if(minTime[adjNode] > time + travelTime) {
// Update the time to reach adjacent node
minTime[adjNode] = time + travelTime;
// Update the number of ways
ways[adjNode] = ways[node];
// Add the new element in priority queue
pq.push({minTime[adjNode] , adjNode});
}
/* Else if the current time taken is same as
earlier known time to reach adjacent node */
else if(minTime[adjNode] == time + travelTime) {
/* Update the number of ways
to reach adjacent nodes */
ways[adjNode] = (ways[adjNode] + ways[node]) % mod;
}
}
}
// Return the result
return ways[n-1] % mod;
}
};
int main() {
int n = 7, m = 20;
vector<vector<int>> roads = {
{0,6,7},{0,1,2},{1,2,3},
{1,3,3},{6,3,3},{3,5,1},
{6,5,1},{2,5,1},{0,4,5},
{4,6,2}
};
/* Creating an instance of
Solution class */
Solution sol;
/* Function call to get the number of ways to
arrive at destinations in shortest possible time */
int ans = sol.countPaths(n, roads);
// Output
cout << "The number of ways to arrive at destinations in shortest possible time is: " << ans;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111
import java.util.*;
class Solution {
/* Function to get the number of ways to arrive
at destinations in shortest possible time */
public int countPaths(int n, List<List<Integer>> roads) {
int mod = 1000000007; // Mod value
// To store the graph
List<int[]>[] adj = new ArrayList[n];
for (int i = 0; i < n; i++) {
adj[i] = new ArrayList<>();
}
// Adding the edges to the graph
for (List<Integer> it : roads) {
adj[it.get(0)].add(new int[]{it.get(1), it.get(2)});
adj[it.get(1)].add(new int[]{it.get(0), it.get(2)});
}
/* Array to store the minimum
time to get to nodes */
long[] minTime = new long[n];
Arrays.fill(minTime, Long.MAX_VALUE);
/* To store the number of
ways to reach nodes */
int[] ways = new int[n];
// Priority queue to store: {time, node}
PriorityQueue<long[]> pq =
new PriorityQueue<>(Comparator.comparingLong(a -> a[0]));
// Initial configuration
minTime[0] = 0;
ways[0] = 1;
pq.add(new long[]{0, 0});
// Until the priority queue is empty
while (!pq.isEmpty()) {
// Get the element
long[] p = pq.poll();
long time = p[0]; // time
int node = (int) p[1]; // node
// Traverse its neighbors
for (int[] it : adj[node]) {
int adjNode = it[0]; // adjacent node
int travelTime = it[1]; // travel time
/* If the current time taken is less than
earlier known time to reach adjacent node */
if (minTime[adjNode] > time + travelTime) {
// Update the time to reach adjacent node
minTime[adjNode] = time + travelTime;
// Update the number of ways
ways[adjNode] = ways[node];
// Add the new element in priority queue
pq.add(new long[]{minTime[adjNode], adjNode});
}
/* Else if the current time taken is same as
earlier known time to reach adjacent node */
else if (minTime[adjNode] == time + travelTime) {
/* Update the number of ways
to reach adjacent nodes */
ways[adjNode] = (ways[adjNode] + ways[node]) % mod;
}
}
}
// Return the result
return ways[n - 1] % mod;
}
public static void main(String[] args) {
int n = 7, m = 20;
List<List<Integer>> roads = Arrays.asList(
Arrays.asList(0, 6, 7),
Arrays.asList(0, 1, 2),
Arrays.asList(1, 2, 3),
Arrays.asList(1, 3, 3),
Arrays.asList(6, 3, 3),
Arrays.asList(3, 5, 1),
Arrays.asList(6, 5, 1),
Arrays.asList(2, 5, 1),
Arrays.asList(0, 4, 5),
Arrays.asList(4, 6, 2)
);
/* Creating an instance of
Solution class */
Solution sol = new Solution();
/* Function call to get the number of ways to
arrive at destinations in shortest possible time */
int ans = sol.countPaths(n, roads);
// Output
System.out.println("The number of ways to arrive at destinations in shortest possible time is: " + ans);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990
import heapq
from collections import defaultdict
from typing import List
class Solution:
# Function to get the number of ways to arrive
# at destinations in shortest possible time
def countPaths(self, n: int, roads: List[List[int]]) -> int:
mod = 10**9 + 7 # Mod value
# To store the graph
adj = defaultdict(list)
# Adding the edges to the graph
for it in roads:
adj[it[0]].append((it[1], it[2]))
adj[it[1]].append((it[0], it[2]))
# Array to store the minimum
# time to get to nodes
minTime = [float('inf')] * n
# To store the number of
# ways to reach nodes
ways = [0] * n
# Priority queue to store: {time, node}
pq = []
# Initial configuration
minTime[0] = 0
ways[0] = 1
heapq.heappush(pq, (0, 0))
# Until the priority queue is empty
while pq:
# Get the element
time, node = heapq.heappop(pq)
# Traverse its neighbors
for adjNode, travelTime in adj[node]:
# If the current time taken is less than
# earlier known time to reach adjacent node
if minTime[adjNode] > time + travelTime:
# Update the time to reach adjacent node
minTime[adjNode] = time + travelTime
# Update the number of ways
ways[adjNode] = ways[node]
# Add the new element in priority queue
heapq.heappush(pq, (minTime[adjNode], adjNode))
# Else if the current time taken is same as
# earlier known time to reach adjacent node
elif minTime[adjNode] == time + travelTime:
# Update the number of ways
# to reach adjacent nodes
ways[adjNode] = (ways[adjNode] + ways[node]) % mod
# Return the result
return ways[n - 1] % mod
# Example usage
if __name__ == "__main__":
n = 7
roads = [
[0, 6, 7], [0, 1, 2], [1, 2, 3],
[1, 3, 3], [6, 3, 3], [3, 5, 1],
[6, 5, 1], [2, 5, 1], [0, 4, 5],
[4, 6, 2]
]
# Creating an instance of
# Solution class
sol = Solution()
# Function call to get the number of ways to
# arrive at destinations in shortest possible time
ans = sol.countPaths(n, roads)
# Output
print("The number of ways to arrive at destinations in shortest possible time is:", ans)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165
// Class implementation Min heap
class MinPriorityQueue {
constructor() {
this.heap = [];
}
isEmpty() {
return this.heap.length === 0;
}
enqueue(element) {
this.heap.push(element);
this.bubbleUp();
}
dequeue() {
if (this.heap.length === 1) {
return this.heap.pop();
}
const top = this.heap[0];
this.heap[0] = this.heap.pop();
this.bubbleDown();
return top;
}
bubbleUp() {
let index = this.heap.length - 1;
const element = this.heap[index];
while (index > 0) {
const parentIndex = Math.floor((index - 1) / 2);
const parent = this.heap[parentIndex];
if (element[0] >= parent[0]) break;
this.heap[index] = parent;
index = parentIndex;
}
this.heap[index] = element;
}
bubbleDown() {
let index = 0;
const length = this.heap.length;
const element = this.heap[index];
while (true) {
let leftChildIndex = 2 * index + 1;
let rightChildIndex = 2 * index + 2;
let leftChild, rightChild;
let swapIndex = null;
if (leftChildIndex < length) {
leftChild = this.heap[leftChildIndex];
if (leftChild[0] < element[0]) {
swapIndex = leftChildIndex;
}
}
if (rightChildIndex < length) {
rightChild = this.heap[rightChildIndex];
if (
(swapIndex === null && rightChild[0] < element[0]) ||
(swapIndex !== null && rightChild[0] < leftChild[0])
) {
swapIndex = rightChildIndex;
}
}
if (swapIndex === null) break;
this.heap[index] = this.heap[swapIndex];
index = swapIndex;
}
this.heap[index] = element;
}
}
class Solution {
/* Function to get the number of ways to arrive
at destinations in shortest possible time */
countPaths(n, roads) {
const mod = 1e9 + 7; // Mod value
// To store the graph
const adj = Array.from({ length: n }, () => []);
// Adding the edges to the graph
for (const it of roads) {
adj[it[0]].push([it[1], it[2]]);
adj[it[1]].push([it[0], it[2]]);
}
/* Array to store the minimum
time to get to nodes */
const minTime = Array(n).fill(Infinity);
/* To store the number of
ways to reach nodes */
const ways = Array(n).fill(0);
// Priority queue to store: {time, node}
const pq = new MinPriorityQueue();
// Initial configuration
minTime[0] = 0;
ways[0] = 1;
pq.enqueue([0, 0]);
// Until the priority queue is empty
while (!pq.isEmpty()) {
// Get the element
const [time, node] = pq.dequeue();
// Traverse its neighbors
for (const [adjNode, travelTime] of adj[node]) {
/* If the current time taken is less than
earlier known time to reach adjacent node */
if (minTime[adjNode] > time + travelTime) {
// Update the time to reach adjacent node
minTime[adjNode] = time + travelTime;
// Update the number of ways
ways[adjNode] = ways[node];
// Add the new element in priority queue
pq.enqueue([minTime[adjNode], adjNode]);
}
/* Else if the current time taken is same as
earlier known time to reach adjacent node */
else if (minTime[adjNode] === time + travelTime) {
/* Update the number of ways
to reach adjacent nodes */
ways[adjNode] = (ways[adjNode] + ways[node]) % mod;
}
}
}
// Return the result
return ways[n - 1] % mod;
}
}
// Example usage
const n = 7;
const roads = [
[0, 6, 7], [0, 1, 2], [1, 2, 3],
[1, 3, 3], [6, 3, 3], [3, 5, 1],
[6, 5, 1], [2, 5, 1], [0, 4, 5],
[4, 6, 2]
];
/* Creating an instance of
Solution class */
const sol = new Solution();
/* Function call to get the number of ways to
arrive at destinations in shortest possible time */
const ans = sol.countPaths(n, roads);
// Output
console.log("The number of ways to arrive at destinations in shortest possible time is: " + ans);
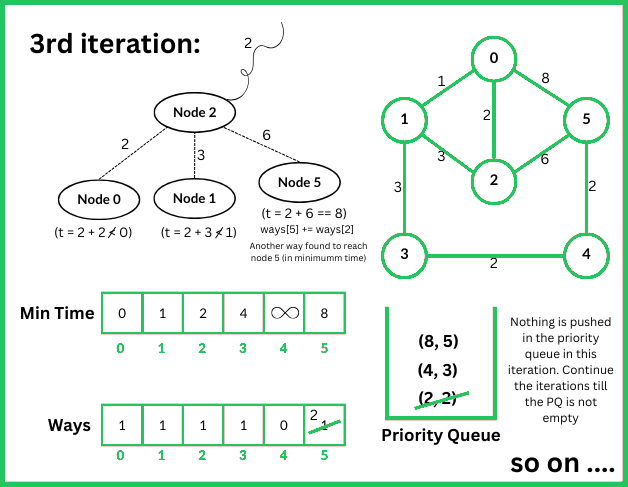
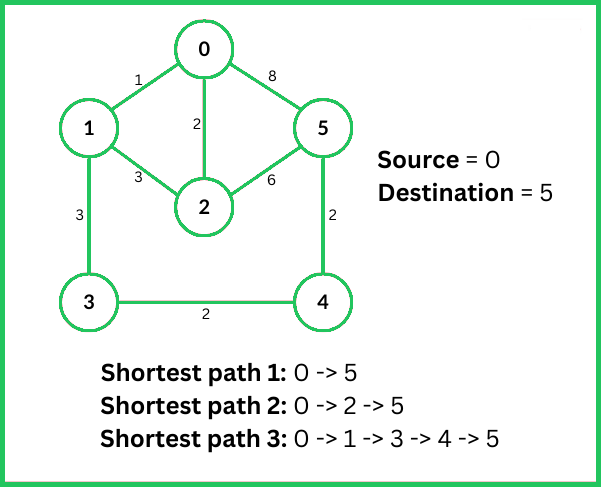which represents that there are three shortest paths to reach the destination node from the source node. 
