Kth element of 2 sorted arrays
Binary Search
FAQs
Hard
Given two sorted arrays a and b of size m and n respectively. Find the kth element of the final sorted array.
Examples:
Input: a = [2, 3, 6, 7, 9], b = [1, 4, 8, 10], k = 5
Output: 6
Explanation: The final sorted array would be [1, 2, 3, 4, 6, 7, 8, 9, 10]. The 5th element of this array is 6.
Input: a = [100, 112, 256, 349, 770], b = [72, 86, 113, 119, 265, 445, 892], k = 7
Output: 256
Explanation: Final sorted array is - [72, 86, 100, 112, 113, 119, 256, 265, 349, 445, 770, 892], 7th element of this array is 256.
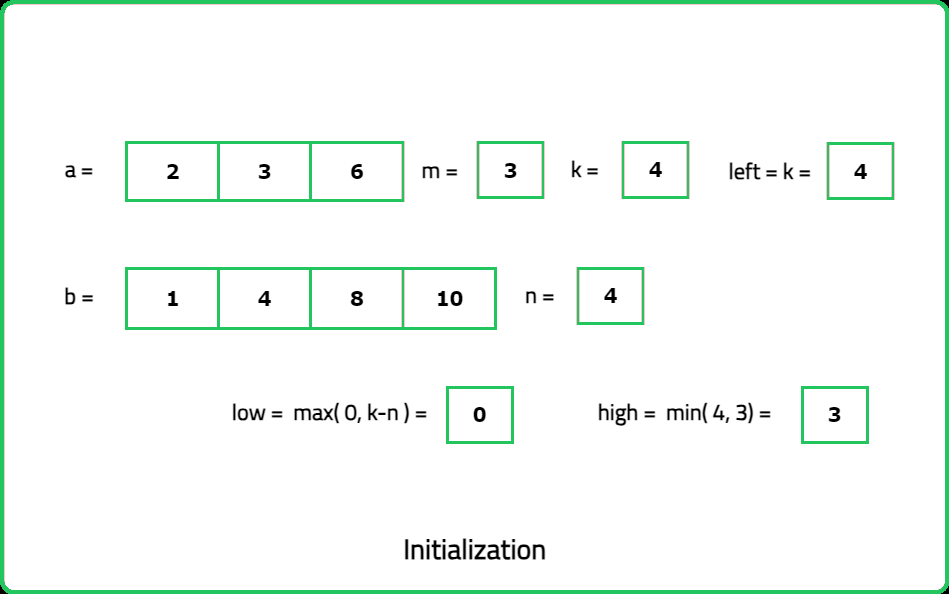
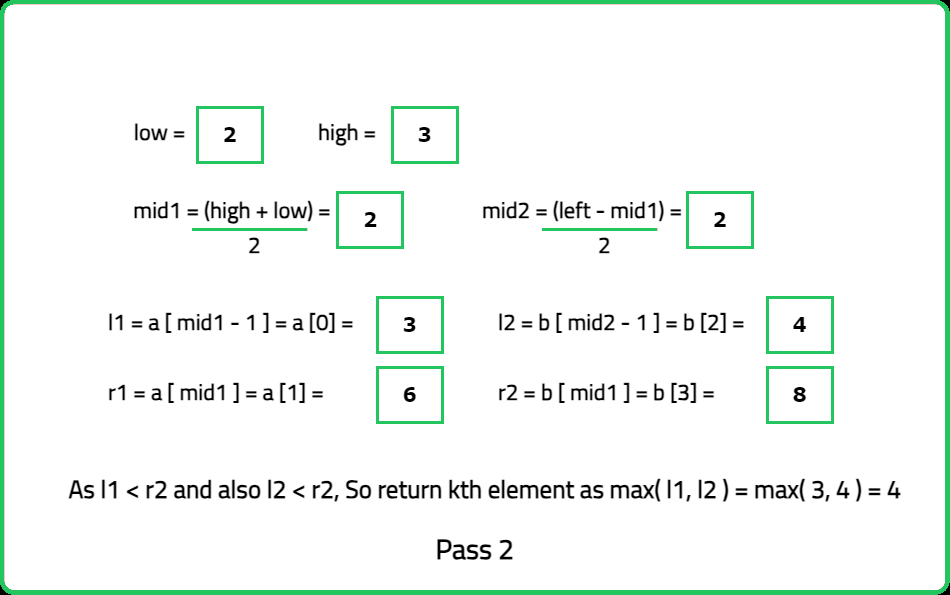
Input: a = [2, 3, 6], b = [7, 9], k = 4
Constraints
- 1 <= m, m <= 104
- 0 <= arr1[i[, arr2[i] < 109
- 1 <= k <= m+n
Hints
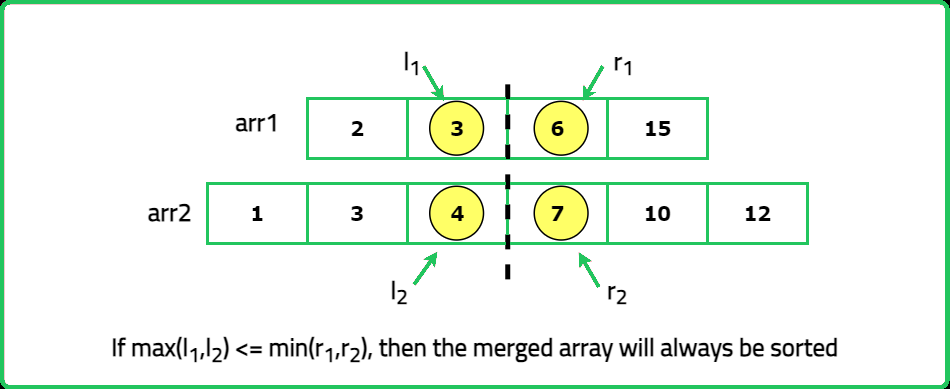
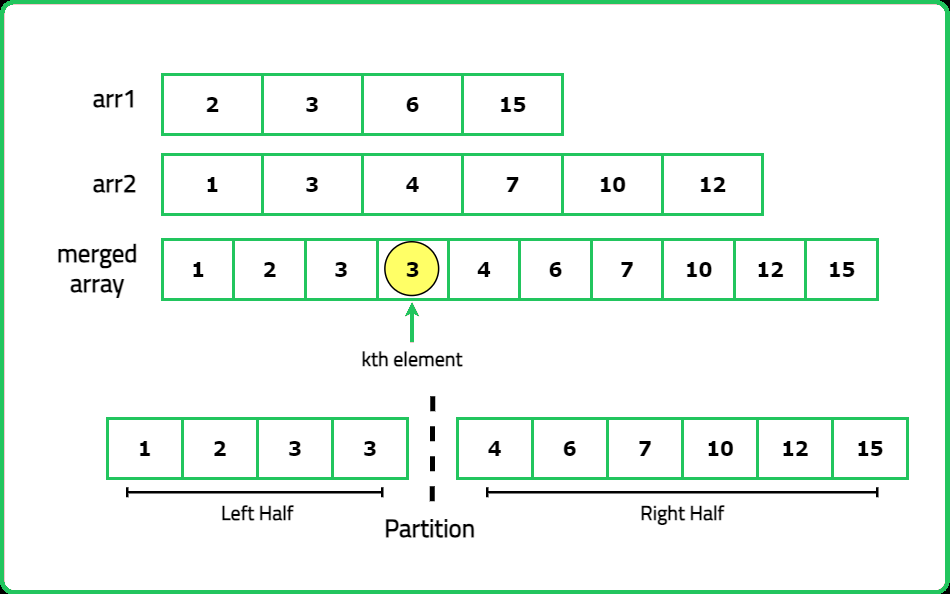
- "At each step, calculate the partition indices for both arrays: Let i be the number of elements taken from array a, so j=k−i elements are taken from array b."
- Ensure that the largest element in the left half is less than or equal to the smallest element in the right half. If valid, the k-th element is the maximum of the last element in the left half
Company Tags
Visa
Flipkart
Unity Technologies
Etsy
DoorDash
eBay
Wayfair
Stripe
Walmart
Western Digital
OYO Rooms
Ernst & Young
Red Hat
ARM
Electronic Arts
Zomato
Uber
Nutanix
PwC
Alibaba
Epic Games
Docker
Rockstar Games
Epic Systems
Robinhood
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe