Sort an array of 0's 1's and 2's
Arrays
FAQs(Medium)
Medium
- This problem, known as the Dutch National Flag problem, is actually quite common in software development
- For instance, a practical application of the solution to this problem is in image processing, specifically in sorting the pixels by color
- When working with RGB (Red, Green, Blue) pixel values, the colors can be classified into three categories (0, 1, 2), and therefore may need to be sorted in a similar manner for different image manipulation techniques
- The key here is that the sorting procedure must not create a new copy of the pixel data (to save memory), which is parallel to the in-place sorting constraint in the problem
Given an array nums consisting of only 0, 1, or 2. Sort the array in non-decreasing order. The sorting must be done in-place, without making a copy of the original array.
Examples:
Input: nums = [1, 0, 2, 1, 0]
Output: [0, 0, 1, 1, 2]
Explanation: The nums array in sorted order has 2 zeroes, 2 ones and 1 two
Input: nums = [0, 0, 1, 1, 1]
Output: [0, 0, 1, 1, 1]
Explanation: The nums array in sorted order has 2 zeroes, 3 ones and zero twos
Input: nums = [1, 1, 2, 2, 1]
Constraints
- 1 <= nums.length <= 105
- nums consists of 0, 1 and 2 only.
Hints
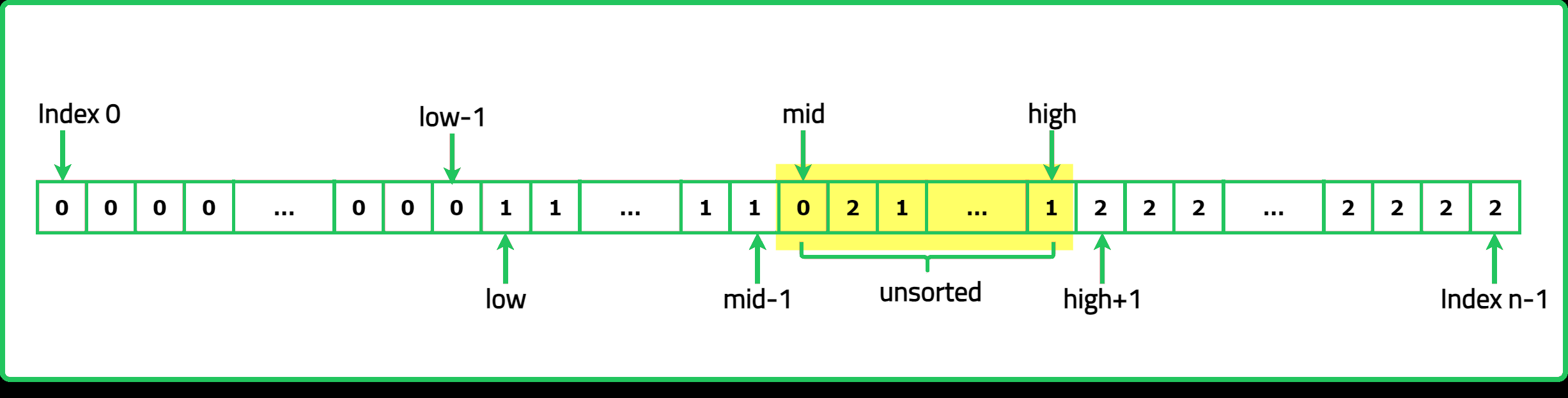
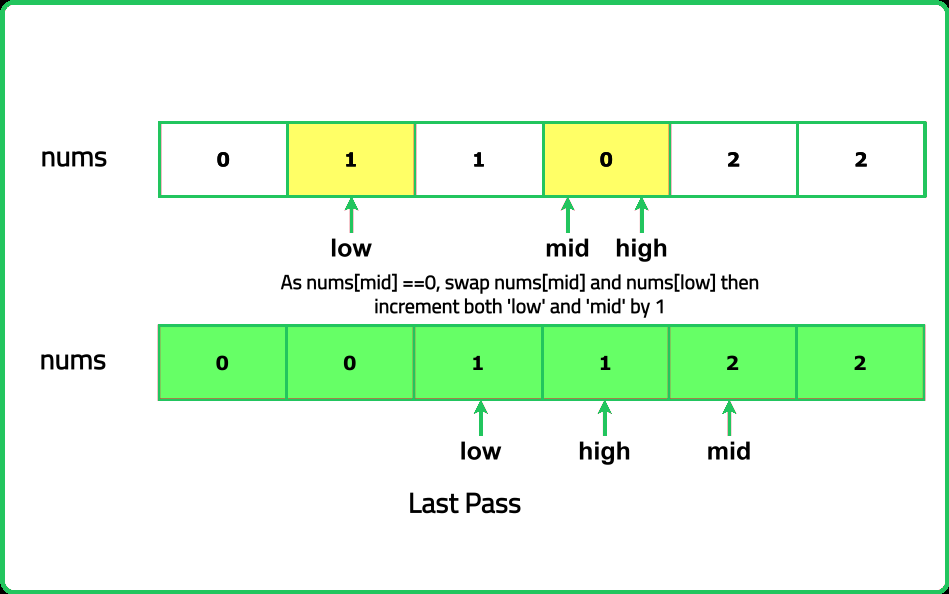
- "Use three pointers (low, mid, and high) to partition the array into three regions: Elements less than 1 (0) are moved to the left (region of 0s). Elements equal to 1 are in the middle. Elements greater than 1 (2) are moved to the right (region of 2s)."
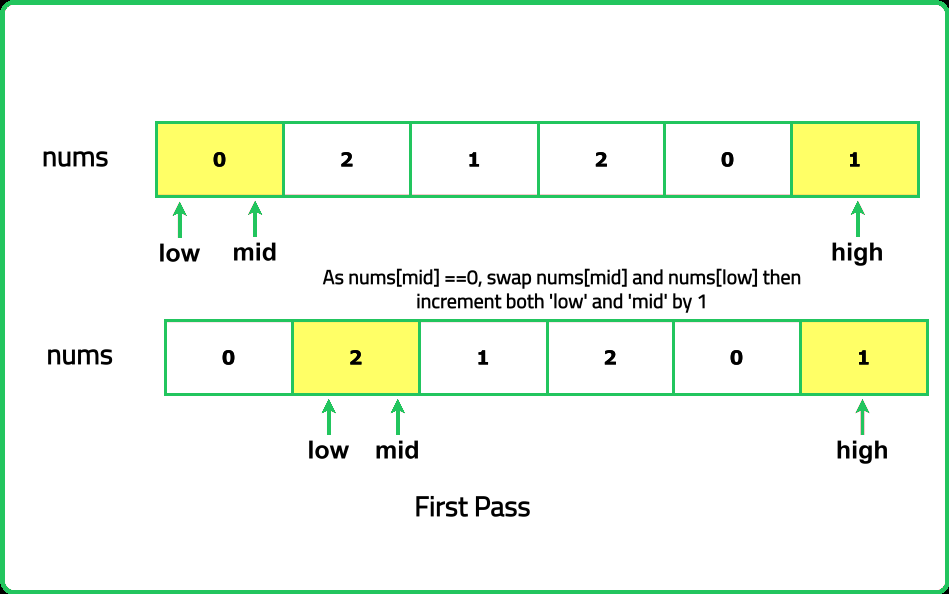
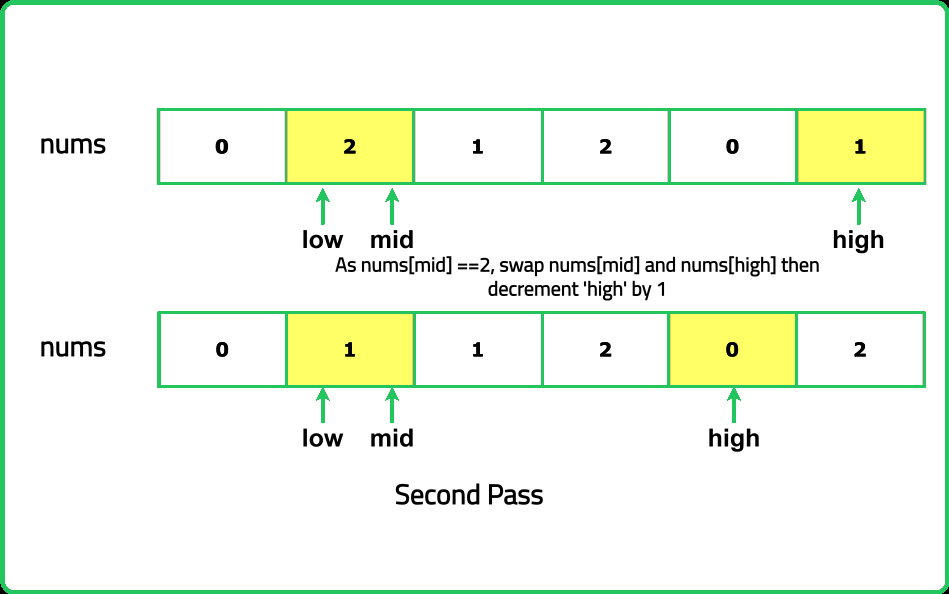
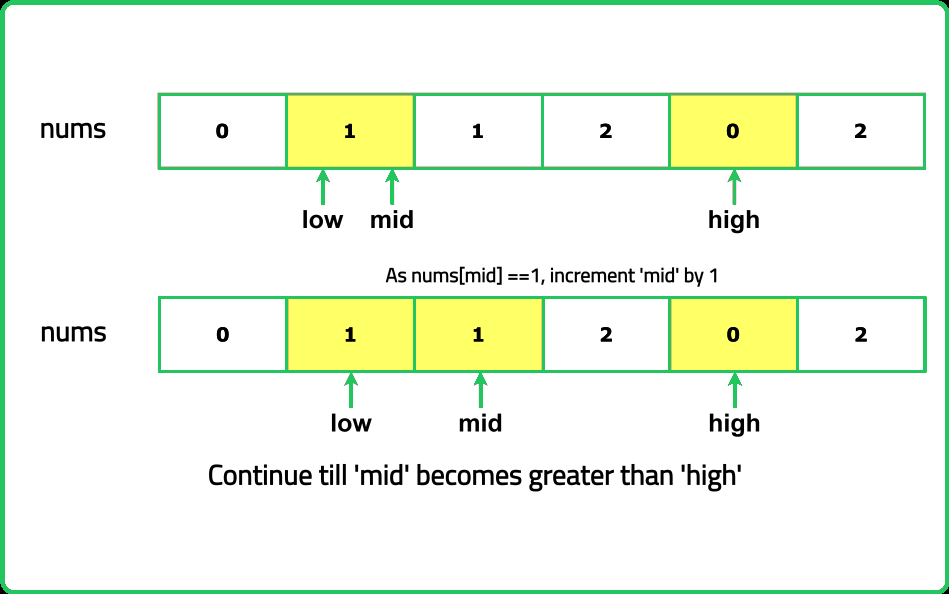
- "If the element at mid is 0, swap it with the element at low and move both pointers forward. If the element at mid is 1, move the mid pointer forward. If the element at mid is 2, swap it with the element at high and move high backward."
Company Tags
Flipkart
Roblox
MongoDB
JPMorgan Chase
Boston Consulting Group
Robinhood
Broadcom
Square
Swiggy
Qualcomm
Reddit
Docker
NVIDIA
PwC
McKinsey & Company
Epic Systems
Red Hat
Rakuten
Morgan Stanley
Bloomberg
Byju's
Western Digital
Seagate Technology
AMD
KPMG
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe