Ninja's training

Why greedy approach will not work:

As the question asks to maximizing points, the initial approach that comes to mind is the greedy approach. The greedy strategy involves selecting the task with the maximum points each day, ensuring that the same task isn't repeated from the previous day. However, following this approach consistently may result in missing out on tasks that offer higher total points over time.

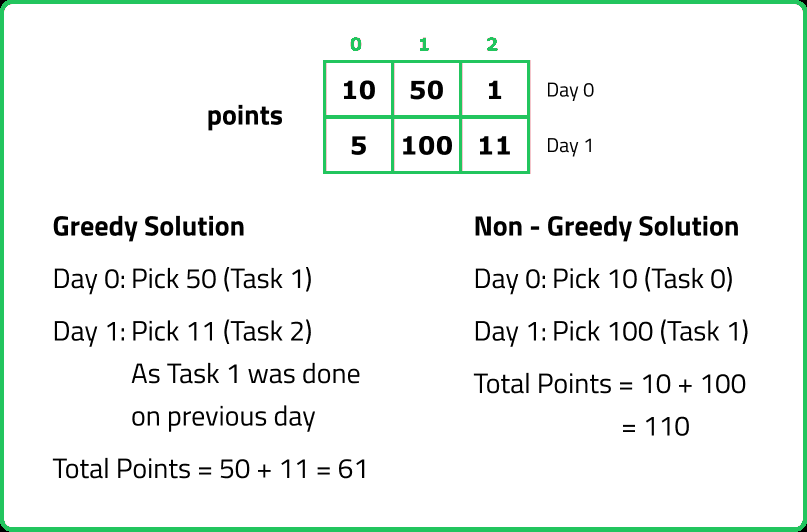
So, we observe that the greedy solution imposes restrictions on our choices, we can lose activity with better points on the next day in the greedy solution. Therefore, it is more advantageous to explore all possible choices as our next solution. We will employ recursion to generate all possible options.

Steps to form the recursive solution:

Express the problem in terms of indexes: On observation we find that the number of days(day0, day1 etc) breaks the problem in different steps. Clearly, we have n days (from 0 to n-1), so one changing parameter which can be expressed in terms of indexes is ‘day’.

Every day we have the option of three activities(say 0,1,2) to be performed. Suppose that we are at a day_i. So we must know the task that was performed on the last day so that we do not repeat it on the present day. It is the ‘last’ choice that we tried out on day_i+1 ( i+1 in case of top-down recursion). Unless we know the last choice we made, we can not decide whether a choice we are making is correct or not.

Now there are three options each day(say 0,1,2) which becomes the ‘last’ of the next day. If we are just starting from the day(n-1), then for this day we can try all three options. We can say ‘last’ for this day is 3, which means any activity can be performed.

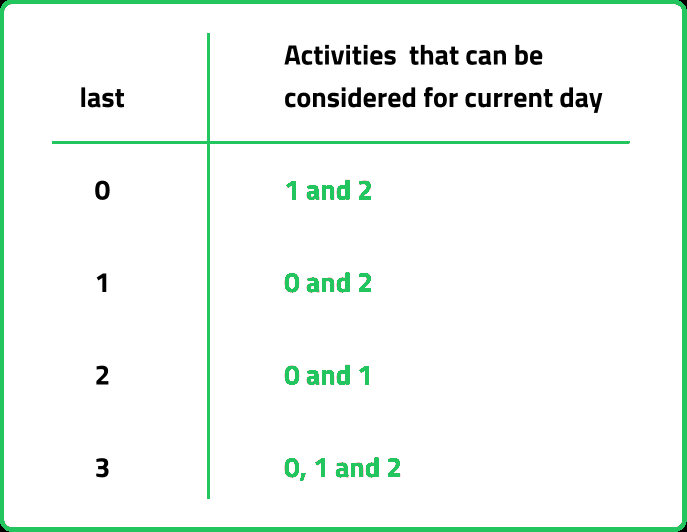
Therefore our function will take two parameters - day and last. f(day, last) will give the maximum points that can be made from day 'day' to day '0', keeping in check that the last activity is not being repeated on consecutive days.

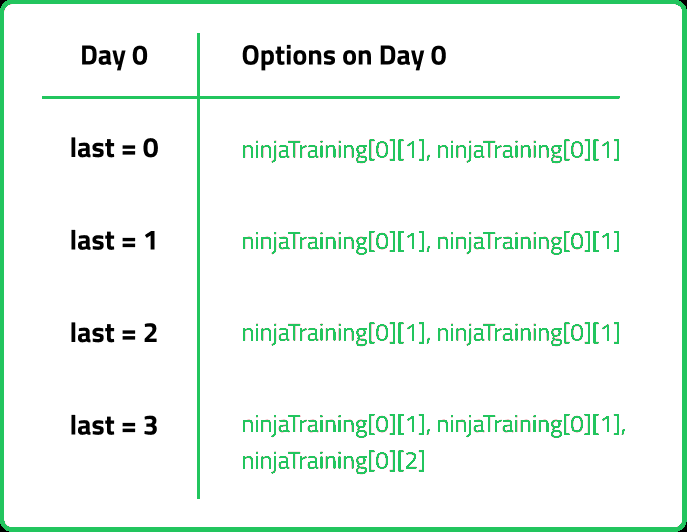
Try out all possible choices at a given index: We are writing a top-down recursive function. We start from day_n-1 to day_0. Therefore whenever we call the recursive function for the next day we call it for f(day-1, last). Now let’s discuss the second parameter. The choices we have for a current day depend on the ‘last’ variable. If we are at our base case (day=0), we will have the following choices.

Other than the base case, whenever we perform an activity(i), its merit points will be given by points[day][i] and to get merit points of the remaining days we will let recursion do its job by passing f(d-1, i). We are passing the second parameter as i because the current day’s activity will become the next day’s last.

/*It is pseudocode and it is not tied to 
any specific programming language.*/
f(day,last){
    if(day == 0){
        for(int i = 0; i <= 2; i++){
            if(i != last)   //code
        }
    }
    for(int i = 0; i <= 2; i++){
        if(i != last){
            activity = points[day][i] + f(day-1, i)
        }
    }

}

Take the maximum of all choices: As the problem statement wants us to find the maximum merit points, take the maximum of all choices.

/*It is pseudocode and it is not tied to 
any specific programming language.*/
f(day,last){
    if(day == 0){
        maxi = 0
        for(int i = 0; i <= 2; i++){
            if(i != last)   maxi = max(maxi,points[0][i]
        }
        return maxi
    } 
    maxi = 0
    for(int i = 0; i <= 2; i++){
        if(i != last){
            activity = points[day][i] + f(day-1, i)
            maxi = max(maxi, activity)
        }
    }
    return maxi

}

Base condition: when the day is 0, preform the activities according to the 'last' and return the maximum points.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Recursive function to calculate the 
    maximum points for the ninja training*/
    int func(int day, int last, vector<vector<int>> &points) {
        // Base case
        if (day == 0) {
            int maxi = 0;
        
            /* Calculate the maximum points for the first day
            by choosing an activity different from last one*/
            for (int i = 0; i <= 2; i++) {
                if (i != last)  maxi = max(maxi, points[0][i]);
            }
        // Return the maximum points
        return maxi;
    }

    int maxi = 0;
    
    // Iterate through activities for the current day
    for (int i = 0; i <= 2; i++) {
        if (i != last) {
            
            /* Calculate the points for the current activity
            and add it to the maximum points obtained so far */
            int activity = points[day][i] + func(day - 1, i, points);
            maxi = max(maxi, activity);
        }
    }

    // Return the maximum points
    return maxi;
}
public:
    int ninjaTraining(vector<vector<int>>& matrix) {
        int day = matrix.size()-1;
        int last = 3;
        return func(day, last, matrix);
    }
};
int main() {
    vector<vector<int>> points = {{10, 40, 70},
                                 {20, 50, 80},
                                 {30, 60, 90}};
    //Create an instance of Solution class
    Solution sol;
    
    cout << sol.ninjaTraining(points);
}
import java.util.*;

class Solution {
    /* Recursive function to calculate the 
    maximum points for the ninja training*/
    private int func(int day, int last, int[][] points) {
        // Base case
        if (day == 0) {
            int maxi = 0;
        
            /* Calculate the maximum points for the first day
            by choosing an activity different from last one*/
            for (int i = 0; i < 3; i++) {
                if (i != last) {
                    maxi = Math.max(maxi, points[0][i]);
                }
            }
            // Return the maximum points for the first day
            return maxi;
        }

        // Initialize max points for the current day
        int maxi = 0;
        
        // Iterate through activities for the current day
        for (int i = 0; i < 3; i++) {
            if (i != last) {
                /* Calculate the points for the current activity
                and add it to the maximum points obtained so far */
                int activity = points[day][i] + func(day - 1, i, points);
                maxi = Math.max(maxi, activity);
            }
        }

        // Return the maximum points for the current day
        return maxi;
    }

    // Function to find the maximum points for ninja training
    public int ninjaTraining(int[][] points) {
        // Get the number of days
        int days = points.length;
        
        // Return the maximum points
        return func(days - 1, 3, points);
    }

    public static void main(String[] args) {
        int[][] points = {
            {10, 40, 70},
            {20, 50, 80},
            {30, 60, 90}
        };

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the maximum points for ninja training
        System.out.println(sol.ninjaTraining(points));
    }
}
class Solution:
    """ Recursive function to calculate the 
    maximum points for the ninja training"""
    def func(self, day, last, points):
        # Base case
        if day == 0:
            maxi = 0
        
            """ Calculate the maximum points for the first day
            by choosing an activity different from last one"""
            for i in range(3):
                if i != last:
                    maxi = max(maxi, points[0][i])
            # Return the maximum points for the first day
            return maxi

        # Initialize max points for the current day
        maxi = 0
        
        # Iterate through activities for the current day
        for i in range(3):
            if i != last:
                """Calculate the points for the current activity
                and add it to the maximum points obtained so far"""
                activity = points[day][i] + self.func(day - 1, i, points)
                maxi = max(maxi, activity)

        # Return the maximum points for the current day
        return maxi

    # Function to find the maximum points for ninja training
    def ninjaTraining(self, points):
        # Get the number of days
        days = len(points)
        
        # If there are no days, return 0
        if days == 0:
            return 0

        # Return the maximum points
        return self.func(days - 1, 3, points)

points = [
    [10, 40, 70],
    [20, 50, 80],
    [30, 60, 90]
]

# Create an instance of Solution class
sol = Solution()

# Print the maximum points for ninja training
print(sol.ninjaTraining(points))
class Solution {
    /* Recursive function to calculate the 
    maximum points for the ninja training*/
    func(day, last, points) {
        // Base case
        if (day === 0) {
            let maxi = 0;
        
            /* Calculate the maximum points for the first day
            by choosing an activity different from last one*/
            for (let i = 0; i < 3; i++) {
                if (i !== last) {
                    maxi = Math.max(maxi, points[0][i]);
                }
            }
            // Return the maximum points for the first day
            return maxi;
        }

        // Initialize max points for the current day
        let maxi = 0;
        
        // Iterate through activities for the current day
        for (let i = 0; i < 3; i++) {
            if (i !== last) {
                /* Calculate the points for the current activity
                and add it to the maximum points obtained so far*/
                let activity = points[day][i] + this.func(day - 1, i, points);
                maxi = Math.max(maxi, activity);
            }
        }

        // Return the maximum points for the current day
        return maxi;
    }

    // Function to find the maximum points for ninja training
    ninjaTraining(points) {
        // Get the number of days
        let days = points.length;
        
        // If there are no days, return 0
        if (days === 0) return 0;

        // Return the maximum points
        return this.func(days - 1, 3, points);
    }
}

let points = [
    [10, 40, 70],
    [20, 50, 80],
    [30, 60, 90]
];

// Create an instance of Solution class
let sol = new Solution();

// Print the maximum points for ninja training
console.log(sol.ninjaTraining(points));

Complexity Analysis:

Time Complexity: O(3^N), where N is the given size of 2D array. Exponential time complexity due to the recursive nature where each day can have up to 3 choices.

Space Complexity:O(N), As the recursion depth is equal to the number of days (days). Therefore, the maximum depth of the recursion stack is O(N).

If we draw the recursion tree, we will see that there are overlapping subproblems. Hence DP approaches can be applied on the recursive solution.

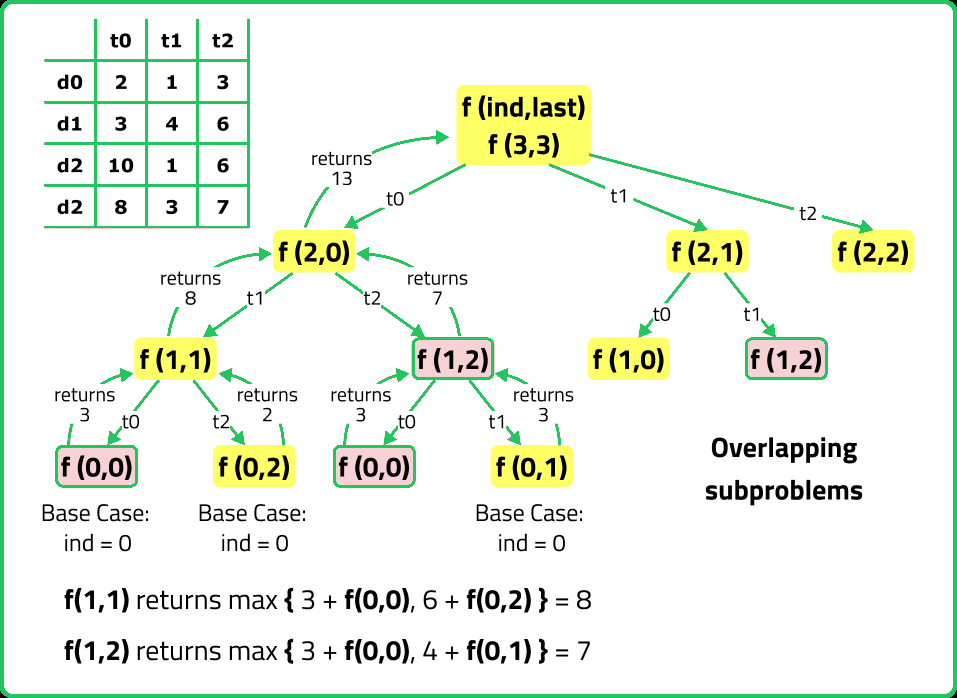
In order to convert a recursive solution to memoization the following steps will be taken:

Declare a dp array of size [n][4]: As there are two parameters in the recursive solution which are changing, first one is 'day' and the other one is 'last'. There are total ‘n’ days and for every day, there can be 4 choices (0,1,2 and 3). Therefore we take the dp array as dp[n][4].

It represents the solution to the subproblem for any given index. Initially, fill the array with -1, to indicate that no subproblem has been solved yet.

While encountering an overlapping subproblem: When we come across a subproblem, for which the dp array has value other than -1, it means we have found a subproblem which has been solved before hence it is an overlapping subproblem. No need to calculate it's value again just retrieve the value from dp array and return it.

Store the value of subproblem: Whenever, a subproblem is enocountered and it is not solved yet(the value at this index will be -1 in the dp array), store the calculated value of subproblem in the array.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    /* Recursive function to calculate the 
    maximum points for the ninja training*/
    int func(int day, int last, vector<vector<int>> &points, vector<vector<int>> &dp) {
        /* If the result for this day and last 
        activity is already calculated, return it*/
        if (dp[day][last] != -1) return dp[day][last];
        
        // Base case
        if (day == 0) {
            int maxi = 0;
        
            /* Calculate the maximum points for the first day
            by choosing an activity different from last one*/
            for (int i = 0; i <= 2; i++) {
                if (i != last)  maxi = max(maxi, points[0][i]);
            }
        // Store the result in dp array and return it
        return dp[day][last] = maxi;
    }

    int maxi = 0;
    
    // Iterate through activities for the current day
    for (int i = 0; i <= 2; i++) {
        if (i != last) {
            
            /* Calculate the points for the current activity
            and add it to the maximum points obtained so far */
            int activity = points[day][i] + func(day - 1, i, points, dp);
            maxi = max(maxi, activity);
        }
    }

    // Store the result in dp array and return it
    return dp[day][last] = maxi;
}
public:
    int ninjaTraining(vector<vector<int>>& matrix) {
        int day = matrix.size();
        
        /* Create a memoization table 
        to store intermediate results*/
        vector<vector<int>> dp(day, vector<int>(4, -1));
        
        int last = 3;
        return func(day-1, last, matrix, dp);
    }
};
int main() {
    vector<vector<int>> points = {{10, 40, 70},
                                 {20, 50, 80},
                                 {30, 60, 90}};
    //Create an instance of Solution class
    Solution sol;
    
    cout << sol.ninjaTraining(points);
}
import java.util.*;

class Solution {
    /* Recursive function to calculate the 
    maximum points for the ninja training*/
    private int func(int day, int last, int[][] points, int[][] dp) {
        // If the result is already calculated, return it
        if (dp[day][last] != -1) return dp[day][last];
        
        // Base case
        if (day == 0) {
            int maxi = 0;
        
            /* Calculate the maximum points for the first day
            by choosing an activity different from last one*/
            for (int i = 0; i < 3; i++) {
                if (i != last) {
                    maxi = Math.max(maxi, points[0][i]);
                }
            }
            // Store the result in dp array and return it
            return dp[day][last] = maxi;
        }

        // Initialize max points for the current day
        int maxi = 0;
        
        // Iterate through activities for the current day
        for (int i = 0; i < 3; i++) {
            if (i != last) {
                /* Calculate the points for the current activity
                and add it to the maximum points obtained so far */
                int activity = points[day][i] + func(day - 1, i, points, dp);
                maxi = Math.max(maxi, activity);
            }
        }

        // Store the result in dp array and return it
        return dp[day][last] = maxi;
    }

    // Function to find the maximum points for ninja training
    public int ninjaTraining(int[][] points) {
        // Get the number of days
        int days = points.length;
        
        // Initialize a memoization table with -1 values
        int dp[][] = new int[days][4];
        for (int[] row : dp)
            Arrays.fill(row, -1);
            
        // Return the maximum points
        return func(days - 1, 3, points, dp);
    }

    public static void main(String[] args) {
        int[][] points = {
            {10, 40, 70},
            {20, 50, 80},
            {30, 60, 90}
        };

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the maximum points for ninja training
        System.out.println(sol.ninjaTraining(points));
    }
}
class Solution:
    """ Recursive function to calculate the 
    maximum points for the ninja training"""
    def func(self, day, last, points, dp):
        """ Check if the result for this day and 
        last activity is already computed."""
        if dp[day][last] != -1:
            return dp[day][last]
        
        # Base case
        if day == 0:
            maxi = 0
        
            """ Calculate the maximum points for the first day
            by choosing an activity different from last one"""
            for i in range(3):
                if i != last:
                    maxi = max(maxi, points[0][i])
            
            # Store maximum points in the DP table and return it.
            dp[day][last] = maxi
            return dp[day][last]

        # Initialize max points for the current day
        maxi = 0
        
        # Iterate through activities for the current day
        for i in range(3):
            if i != last:
                """Calculate the points for the current activity
                and add it to the maximum points obtained so far"""
                activity = points[day][i] + self.func(day - 1, i, points, dp)
                maxi = max(maxi, activity)

        # Store maximum points in the DP table and return it.
        dp[day][last] = maxi
        return dp[day][last]

    # Function to find the maximum points for ninja training
    def ninjaTraining(self, points):
        # Get the number of days
        days = len(points)
        
        # Initialize a DP table to store the computed results.
        dp = [[-1 for j in range(4)] for i in range(days)]
        
        # If there are no days, return 0
        if days == 0:
            return 0

        # Return the maximum points
        return self.func(days - 1, 3, points, dp)

points = [
    [10, 40, 70],
    [20, 50, 80],
    [30, 60, 90]
]

# Create an instance of Solution class
sol = Solution()

# Print the maximum points for ninja training
print(sol.ninjaTraining(points))  # Output should be 210
class Solution {
    /* Recursive function to calculate the 
    maximum points for the ninja training*/
    func(day, last, points, dp) {
        /* If the result for this day and last 
        activity is already calculated, return it */
        if (dp[day][last] !== -1) return dp[day][last];
        
        // Base case
        if (day === 0) {
            let maxi = 0;
        
            /* Calculate the maximum points for the first day
            by choosing an activity different from last one*/
            for (let i = 0; i < 3; i++) {
                if (i !== last) {
                    maxi = Math.max(maxi, points[0][i]);
                }
            }
            //Store the result in dp array and return it
            dp[day][last] = maxi;
            return dp[day][last];
        }

        // Initialize max points for the current day
        let maxi = 0;
        
        // Iterate through activities for the current day
        for (let i = 0; i < 3; i++) {
            if (i !== last) {
                /* Calculate the points for the current activity
                and add it to the maximum points obtained so far*/
                let activity = points[day][i] + this.func(day - 1, i, points, dp);
                maxi = Math.max(maxi, activity);
            }
        }

        //Store the result in dp array and return it
        dp[day][last] = maxi;
        return dp[day][last];
    }

    // Function to find the maximum points for ninja training
    ninjaTraining(points) {
        // Get the number of days
        let days = points.length;
        
        /* Create a memoization table 
        to store intermediate results*/
        let dp = new Array(days);
        for (let i = 0; i < days; i++) {
            dp[i] = new Array(4).fill(-1);
        }

        // Return the maximum points
        return this.func(days - 1, 3, points, dp);
    }
}

let points = [
    [10, 40, 70],
    [20, 50, 80],
    [30, 60, 90]
];

// Create an instance of Solution class
let sol = new Solution();

// Print the maximum points for ninja training
console.log(sol.ninjaTraining(points));

Complexity Analysis:

Time Complexity: O(N*4*3). There are N*4 states and for every state, we are running a for loop iterating three times.

Space Complexity:O(N) + O(N*4), We are using a recursion stack space(O(N)) and a 2D array (again O(N*4)). Therefore total space complexity will be O(N) + O(N) ≈ O(N)

In order to convert a recursive code to tabulation code, we try to convert the recursive code to tabulation and here are the steps:

Declare a dp array of size [n][4]: There are total ‘n’ days and for every day, there can be 4 choices (0,1,2 and 3). Therefore we take the dp array as dp[n][4] and dp[i][j] represents the maximum points at day i, considering the last activity as j.

Setting Base Cases in the Array: In the recursive code, we knew the answer for base case, when 'day' = 0, Therefore, we can say that the following will be the base conditions

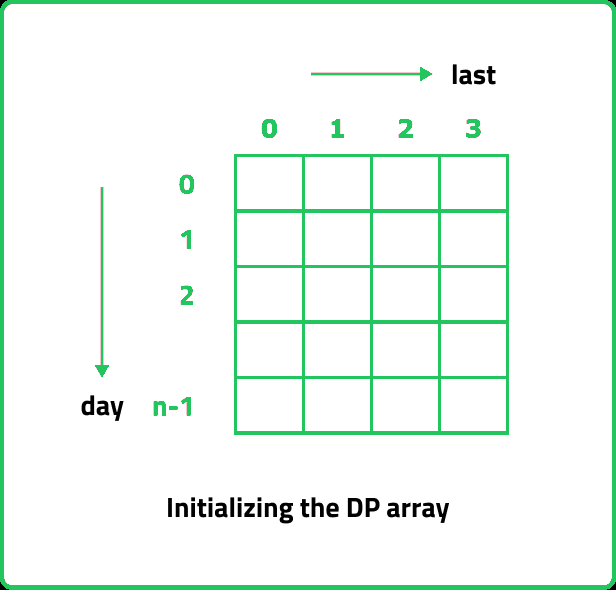
dp[0][0] = max(points[0][1], points[0][2]), when the last activity is 0.

dp[0][1] = max(points[0][0], points[0][2]), when the last activity is 1.

dp[0][2] = max(points[0][0], points[0][1]), when the last activity is 2.

dp[0][3] = max(points[0][0], points[0][1] and points[0][2]), when the last is 3, it means we are just starting from here and no activity has been performed yet.

Iterative Computation Using Loops: Set an iterative loop that traverses the array( from index 1 to n-1), for each day iterate through all the 4 choices of the 'last' and then Iterate through the tasks for the current day. Calculate the points for the current activity and add it to the maximum points obtained on the previous day.

Choosing the maximum: Update dp[day][last] to store the maximum of dp[day][last] and current calculation.

Returning the last element: The last element of the dp array is returned because it holds the optimal solution to the entire problem after the bottom-up computation has been completed.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to calculate the maximum
    points for the ninja training*/
    int ninjaTraining(vector<vector<int>>& matrix) {
        int n = matrix.size();
        // Create a 2D DP table to store the maximum points
        vector<vector<int>> dp(n, vector<int>(4, 0));

       // Initialize the DP table for the first day (day 0)
       dp[0][0] = max(matrix[0][1], matrix[0][2]);
       dp[0][1] = max(matrix[0][0], matrix[0][2]);
       dp[0][2] = max(matrix[0][0], matrix[0][1]);
       dp[0][3] = max(matrix[0][0], max(matrix[0][1], matrix[0][2]));

       // Iterate through the days starting from day 1
       for (int day = 1; day < n; day++) {
           for (int last = 0; last < 4; last++) {
               dp[day][last] = 0;
               // Iterate through the tasks for the current day
               for (int task = 0; task <= 2; task++) {
                   if (task != last) {
                        /* Calculate the points for the current 
                        activity and add it to the maximum points
                        obtained on the previous day */
                        int activity = matrix[day][task] + dp[day - 1][task];
                   
                        /* Update the maximum points for 
                        the current day and last activity*/
                        dp[day][last] = max(dp[day][last], activity);
                    }
                }
            }
       }

       /* The maximum points for the last day with 
       any activity can be found in dp[n-1][3]*/
       return dp[n - 1][3];
    }
};
int main() {
    vector<vector<int>> points = {{10, 40, 70},
                                 {20, 50, 80},
                                 {30, 60, 90}};
                                 
    //Create an instance of Solution class
    Solution sol;
    
    cout << sol.ninjaTraining(points);
}
import java.util.Arrays;

class Solution {
    /* Function to calculate the maximum
    points for the ninja training*/
    public int ninjaTraining(int[][] matrix) {
        int n = matrix.length;
        // Create a 2D DP table to store the maximum points
        int[][] dp = new int[n][4];

        // Initialize the DP table for the first day (day 0)
        dp[0][0] = Math.max(matrix[0][1], matrix[0][2]);
        dp[0][1] = Math.max(matrix[0][0], matrix[0][2]);
        dp[0][2] = Math.max(matrix[0][0], matrix[0][1]);
        dp[0][3] = Math.max(matrix[0][0], Math.max(matrix[0][1], matrix[0][2]));

        // Iterate through the days starting from day 1
        for (int day = 1; day < n; day++) {
            for (int last = 0; last < 4; last++) {
                dp[day][last] = 0;
                // Iterate through the tasks for the current day
                for (int task = 0; task <= 2; task++) {
                    if (task != last) {
                        /* Calculate the points for the current 
                        activity and add it to the maximum points
                        obtained on the previous day */
                        int activity = matrix[day][task] + dp[day - 1][task];

                        /* Update the maximum points for 
                        the current day and last activity*/
                        dp[day][last] = Math.max(dp[day][last], activity);
                    }
                }
            }
        }

        /* The maximum points for the last day with 
        any activity can be found in dp[n-1][3]*/
        return dp[n - 1][3];
    }

    public static void main(String[] args) {
        int[][] points = {
            {10, 40, 70},
            {20, 50, 80},
            {30, 60, 90}
        };
        
        // Create an instance of Solution class
        Solution sol = new Solution();
        
        // Print the maximum points for ninja training
        System.out.println(sol.ninjaTraining(points)); 
    }
}
class Solution:
    """ Function to calculate the maximum
    points for the ninja training"""
    def ninjaTraining(self, matrix):
        n = len(matrix)
        # Create a 2D DP table to store the maximum points
        dp = [[0] * 4 for _ in range(n)]

        # Initialize the DP table for the first day (day 0)
        dp[0][0] = max(matrix[0][1], matrix[0][2])
        dp[0][1] = max(matrix[0][0], matrix[0][2])
        dp[0][2] = max(matrix[0][0], matrix[0][1])
        dp[0][3] = max(matrix[0][0], max(matrix[0][1], matrix[0][2]))

        # Iterate through the days starting from day 1
        for day in range(1, n):
            for last in range(4):
                dp[day][last] = 0
                # Iterate through the tasks for the current day
                for task in range(3):
                    if task != last:
                        """ Calculate the points for the current 
                        activity and add it to the maximum points
                        obtained on the previous day"""
                        activity = matrix[day][task] + dp[day - 1][task]

                        """Update the maximum points for 
                        the current day and last activity"""
                        dp[day][last] = max(dp[day][last], activity)

        """ The maximum points for the last day with 
        any activity can be found in dp[n-1][3]"""
        return dp[n - 1][3]

points = [
    [10, 40, 70],
    [20, 50, 80],
    [30, 60, 90]
]

# Create an instance of Solution class
sol = Solution()

# Print the maximum points for ninja training
print(sol.ninjaTraining(points))  
class Solution {
    /* Function to find the maximum 
    points for ninja training*/
    ninjaTraining(matrix) {
        let n = matrix.length;
        // Create a 2D DP table to store the maximum points
        let dp = new Array(n);
        for (let i = 0; i < n; i++) {
            dp[i] = new Array(4).fill(0);
        }

        // Initialize the DP table for the first day (day 0)
        dp[0][0] = Math.max(matrix[0][1], matrix[0][2]);
        dp[0][1] = Math.max(matrix[0][0], matrix[0][2]);
        dp[0][2] = Math.max(matrix[0][0], matrix[0][1]);
        dp[0][3] = Math.max(matrix[0][0], Math.max(matrix[0][1], matrix[0][2]));

        // Iterate through the days starting from day 1
        for (let day = 1; day < n; day++) {
            for (let last = 0; last < 4; last++) {
                dp[day][last] = 0;
                // Iterate through the tasks for the current day
                for (let task = 0; task < 3; task++) {
                    if (task !== last) {
                        /* Calculate the points for the current 
                        activity and add it to the maximum points
                        obtained on the previous day */
                        let activity = matrix[day][task] + dp[day - 1][task];

                        /* Update the maximum points for 
                        the current day and last activity*/
                        dp[day][last] = Math.max(dp[day][last], activity);
                    }
                }
            }
        }

        /* The maximum points for the last day with 
        any activity can be found in dp[n-1][3]*/
        return dp[n - 1][3];
    }
}

let points = [
    [10, 40, 70],
    [20, 50, 80],
    [30, 60, 90]
];

// Create an instance of Solution class
let sol = new Solution();

// Print the maximum points for ninja training
console.log(sol.ninjaTraining(points)); 

Complexity Analysis:

Time Complexity: O(N*4*3). There are N*4 states and for every state, we are running a for loop iterating three times.

Space Complexity:O(N*4), 2D array is being used to store the intermediate calculations.

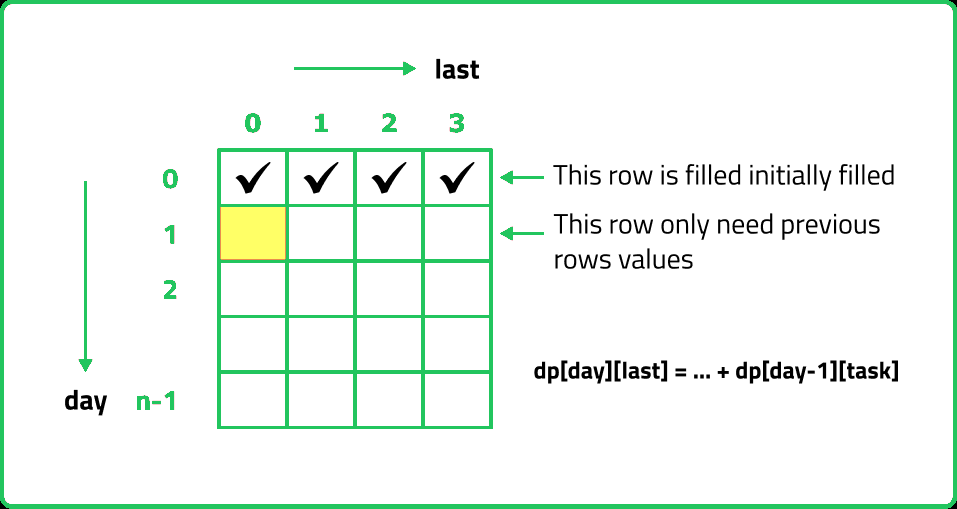
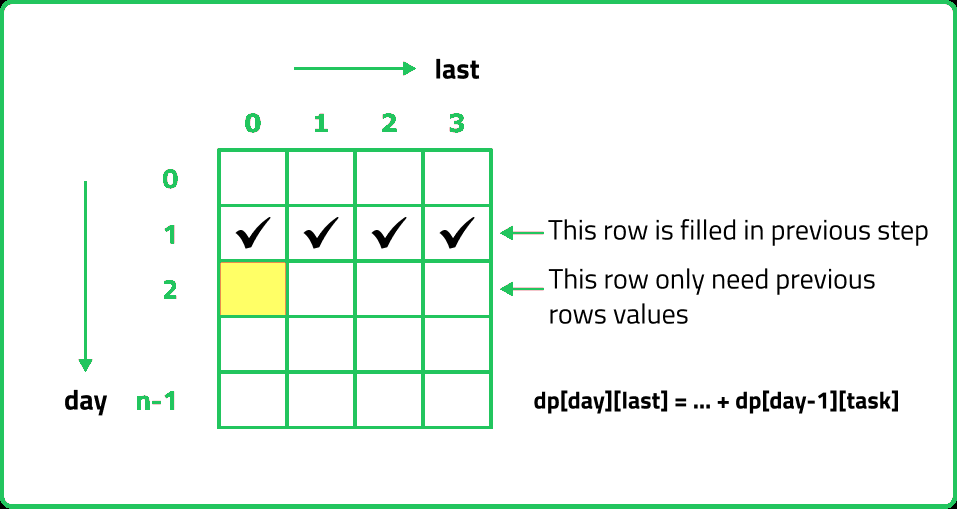
If we closely look the relation obtained in the tabulation approach, dp[day][last] = max(dp[day][last],matrix[day][task] + dp[day-1][task])

Here the task can be anything from 0 to 3 and day-1 is the previous stage of recursion. So in order to compute any dp array value, we only require the last row to calculate it.

So rather than storing the entire 2D Array of size N*4, we can just store values of size 4(say prev).

We can then take a dummy array, again of size 4 (say temp) and calculate the next row’s value using the array we stored in step 1.

After that whenever we move to the next day, the temp array becomes our prev for the next step.

At last prev[3] will give us the answer because it will be the last element, storing the maximum points in bottom-up manner.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to calculate the maximum
    points for the ninja training*/
    int ninjaTraining(vector<vector<int>>& matrix) {
        int n = matrix.size();
        
        /* Initialize a vector to store the maximum
        points for the previous day's activities*/
        vector<int> prev(4, 0);

        // Initialize the prev array for the first day (day 0)
        prev[0] = max(matrix[0][1], matrix[0][2]);
        prev[1] = max(matrix[0][0], matrix[0][2]);
        prev[2] = max(matrix[0][0], matrix[0][1]);
        prev[3] = max(matrix[0][0], max(matrix[0][1], matrix[0][2]));

        // Iterate through the days starting from day 1
        for (int day = 1; day < n; day++) {
            /* Create a temporary vector to store the
            maximum points for the current day's activities*/
            vector<int> temp(4, 0);
            for (int last = 0; last < 4; last++) {
                temp[last] = 0;
                // Iterate through the tasks for the current day
                for (int task = 0; task <= 2; task++) {
                    if (task != last) {
                    /* Calculate the points for the current activity
                    and add it to the maximum points obtained on the
                    previous day (stored in prev)*/
                    temp[last] = max(temp[last], matrix[day][task] + prev[task]);
                }
            }
        }
        // Update prev with maximum points for the current day
        prev = temp;
       }

        /* The maximum points for the last day with 
        any activity can be found in prev[3]*/
        return prev[3];
    }
};
int main() {
    vector<vector<int>> points = {{10, 40, 70},
                                 {20, 50, 80},
                                 {30, 60, 90}};
                                 
    //Create an instance of Solution class
    Solution sol;
    
    cout << sol.ninjaTraining(points);
}
import java.util.Arrays;

class Solution {
    /* Function to calculate the maximum
    points for the ninja training*/
    public int ninjaTraining(int[][] matrix) {
        int n = matrix.length;

         /* Initialize a vector to store the maximum
        points for the previous day's activities*/
        int[] prev = new int[4];

        // Initialize the prev array for the first day (day 0)
        prev[0] = Math.max(matrix[0][1], matrix[0][2]);
        prev[1] = Math.max(matrix[0][0], matrix[0][2]);
        prev[2] = Math.max(matrix[0][0], matrix[0][1]);
        prev[3] = Math.max(matrix[0][0], Math.max(matrix[0][1], matrix[0][2]));

        // Iterate through the days starting from day 1
        for (int day = 1; day < n; day++) {
            /* Initialize a temporary vector to store the
            maximum points for the current day's activities*/
            int[] temp = new int[4];

            for (int last = 0; last < 4; last++) {
                temp[last] = 0;
                // Iterate through the tasks for the current day
                for (int task = 0; task <= 2; task++) {
                    if (task != last) {
                        /* Calculate the points for the current activity
                        and add it to the maximum points obtained on the
                        previous day (stored in prev)*/
                        temp[last] = Math.max(temp[last], matrix[day][task] + prev[task]);
                    }
                }
            }

            // Update prev with maximum points for the current day
            prev = temp;
        }

        /* The maximum points for the last day with 
        any activity can be found in prev[3]*/
        return prev[3];
    }

    public static void main(String[] args) {
        int[][] points = {
            {10, 40, 70},
            {20, 50, 80},
            {30, 60, 90}
        };

        // Create an instance of Solution class
        Solution sol = new Solution();

        // Print the maximum points for ninja training
        System.out.println(sol.ninjaTraining(points)); 
    }
}
class Solution:
    """ Function to calculate the maximum
    points for the ninja training"""
    def ninjaTraining(self, matrix):
        n = len(matrix)

        """ Initialize an array to store the maximum
        points for the previous day's activities"""
        prev = [0] * 4

        # Initialize the prev array for the first day (day 0)
        prev[0] = max(matrix[0][1], matrix[0][2])
        prev[1] = max(matrix[0][0], matrix[0][2])
        prev[2] = max(matrix[0][0], matrix[0][1])
        prev[3] = max(matrix[0][0], max(matrix[0][1], matrix[0][2]))

        # Iterate through the days starting from day 1
        for day in range(1, n):
            """ Initialize a temporary array to store the 
            maximum points for the current day's activities"""
            temp = [0] * 4

            for last in range(4):
                temp[last] = 0
                # Iterate through the tasks for the current day
                for task in range(3):
                    if task != last:
                        """ Calculate the points for the current activity
                        and add it to the maximum points obtained on 
                        the previous day"""
                        temp[last] = max(temp[last], matrix[day][task] + prev[task])

            # Update prev with maximum points for the current day
            prev = temp

        """ The maximum points for the last day with 
        any activity can be found in prev[3]"""
        return prev[3]

points = [
    [10, 40, 70],
    [20, 50, 80],
    [30, 60, 90]
]

# Create an instance of Solution class
sol = Solution()

# Print the maximum points for ninja training
print(sol.ninjaTraining(points))  
class Solution {
    /* Function to calculate the maximum 
    points for the ninja training*/
    ninjaTraining(matrix) {
        let n = matrix.length;

        /* Initialize an array to store the maximum
        points for the previous day's activities*/
        let prev = [0, 0, 0, 0];

        // Initialize the prev array for the first day (day 0)
        prev[0] = Math.max(matrix[0][1], matrix[0][2]);
        prev[1] = Math.max(matrix[0][0], matrix[0][2]);
        prev[2] = Math.max(matrix[0][0], matrix[0][1]);
        prev[3] = Math.max(matrix[0][0], Math.max(matrix[0][1], matrix[0][2]));

        // Iterate through the days starting from day 1
        for (let day = 1; day < n; day++) {
            /* Initialize a temporary array to store the 
            maximum points for the current day's activities*/
            let temp = [0, 0, 0, 0];

            for (let last = 0; last < 4; last++) {
                temp[last] = 0;
                // Iterate through the tasks for the current day
                for (let task = 0; task <= 2; task++) {
                    if (task !== last) {
                        /* Calculate the points for the current activity
                        and add it to the maximum points obtained on
                        the previous day*/
                        temp[last] = Math.max(temp[last], matrix[day][task] + prev[task]);
                    }
                }
            }

            // Update prev with maximum points for the current day
            prev = temp;
        }

        /* The maximum points for the last day with 
        any activity can be found in prev[3]*/
        return prev[3];
    }
}

let points = [
    [10, 40, 70],
    [20, 50, 80],
    [30, 60, 90]
];

// Create an instance of Solution class
let sol = new Solution();

// Print the maximum points for ninja training
console.log(sol.ninjaTraining(points)); // Output: 210

Complexity Analysis:

Time Complexity: O(N*4*3). There are N*4 states and for every state, we are running a for loop iterating three times.

Space Complexity:O(4), We are using an external array of size ‘4’ to store only one row.

Problem List

Examples:

Constraints

Hints

Company Tags

Editorial

Why greedy approach will not work:

Steps to form the recursive solution:

Complexity Analysis:

Complexity Analysis:

Complexity Analysis:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code