Pre Requisite: DFS traversal technique
What is meant by Strongly Connected Component (SCC)?
A component is called a Strongly Connected Component(SCC) only if for every possible pair of vertices (u, v) inside that component, u is reachable from v and v is reachable from u.
Note: Strongly connected components(SCC) are only valid for directed graphs.
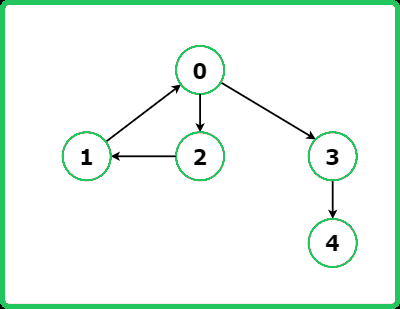
Consider the following example:
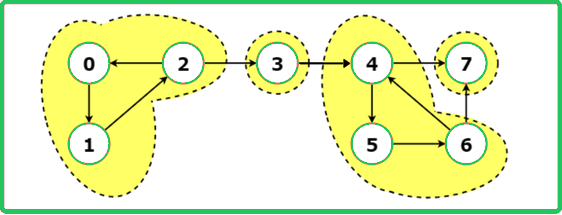
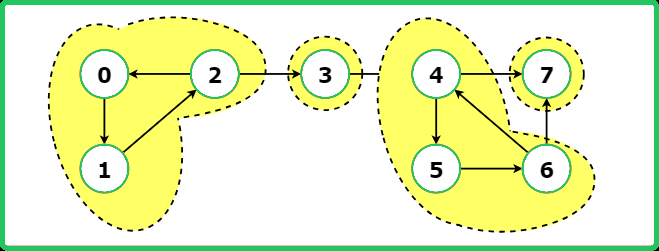
There are 4 strongly connected components in the above graph which are (0,1,2), (3), (4,5,6), and (7). Note that a component containing a single vertex is always a strongly connected component.
Intuition:
Example:
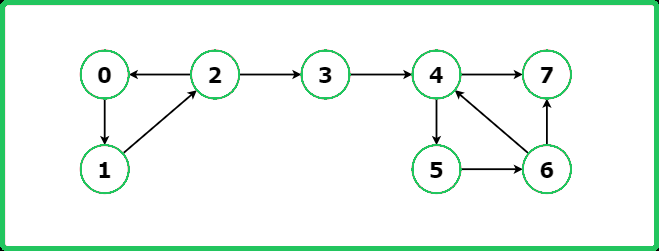
Consider starting a DFS traversal from node 0 for the following graph, it will end up visiting all nodes making it impossible to differentiate between different SCCs:
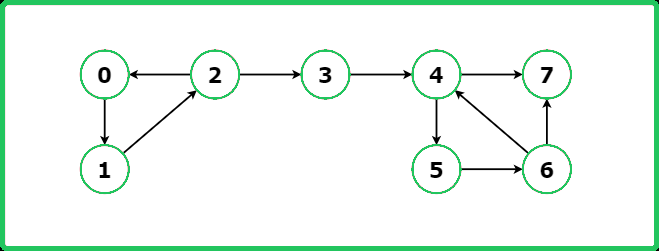
Another way to represent the graph is in the following way:
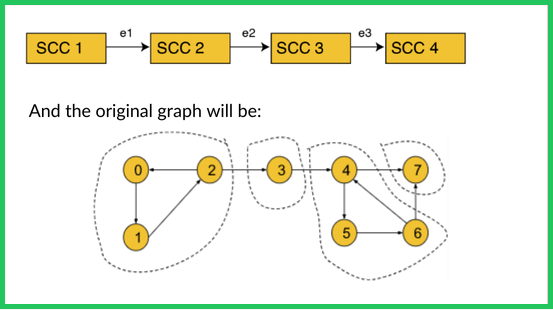
By definition, within each SCC, every node is reachable. So, DFS traversal is started from a node of SCC1, all the nodes in SCC1 can be visited and via edge e1 the SCC2 can be reached. Similarly, traversal can be done from SCC2 to SCC3 via edge e2 and from SCC3 to SCC4 via edge e3. Thus all the nodes of the graph become reachable.
But, if the edges e1, e2, e3 and e4 are reversed, the graph will be:
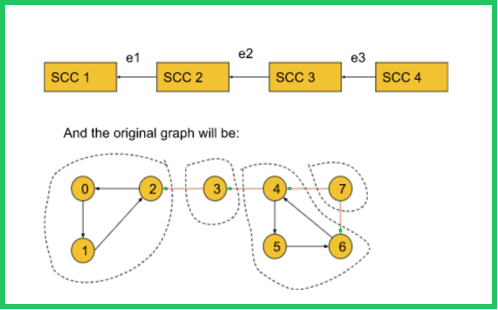
Now, in this graph, if a DFS is started from node 0, it will only visit nodes in SSC1. It is true for all other nodes in Strongly Connected Components. Hence, it is clear that in one DFS call, all the nodes in one SCC will be visited.
Thus, the number of DFS calls will represent the number of strongly connected components.
How to identify the edges that must be reversed?
To find the edges that must be reversed, the strongly connected components must be known prior. To solve this problem, all the edges in the graph can be reversed, this will not affect the strongly connected components as already all nodes are reachable to each other. Thus, the graph will look like this:
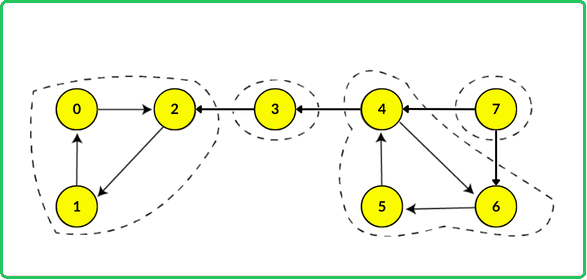
How to identify the starting node for DFS traversal?
Consider if instead of node 0, node 7 is used as the starting node for DFS traversal. In such a case, even after reversing the edges, all the nodes will be visited. Thus, it is important to identify the node from where the DFS can be started so that the SCCs can be identified.
This can be solved by identifying the order of visiting the nodes when a DFS traversal is made on the original graph. The node that will be visited later will have a
greater finishing time, and the node that will be visited before will have a
smaller finishing time.
Using this, the order in which the nodes must be visited to determine the number of SCCs can be determined based on their finishing time. The DFS calls for the node that was visited first(having the smallest finishing time) must be made first and for the node that was visited last(having the greatest finishing time) must be made last.
Note: Since the node visited
last in the original DFS call must be visited
first in the later DFS call, a
Stack data structure can be used to store the nodes based on their finishing times.
Kosaraju's Algorithm:
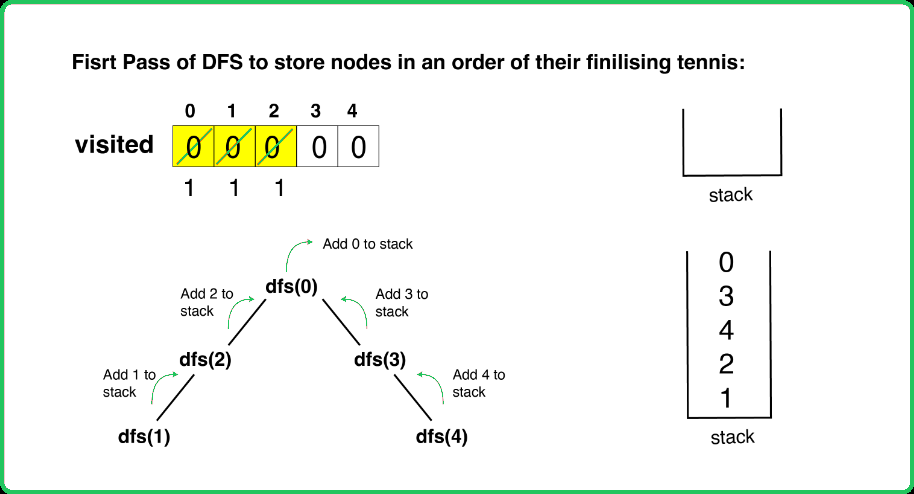
- Sort all the nodes according to their finishing time: Perform a DFS call to sort the nodes based on their finishing time and store them in a stack.
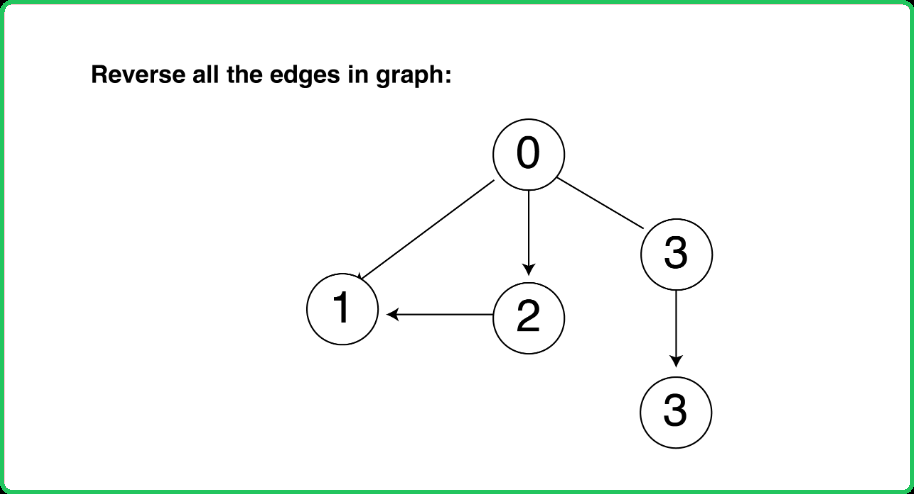
- Reverse all the edges of the entire graph: Create a new graph where all the edges of the original graph will be reversed.
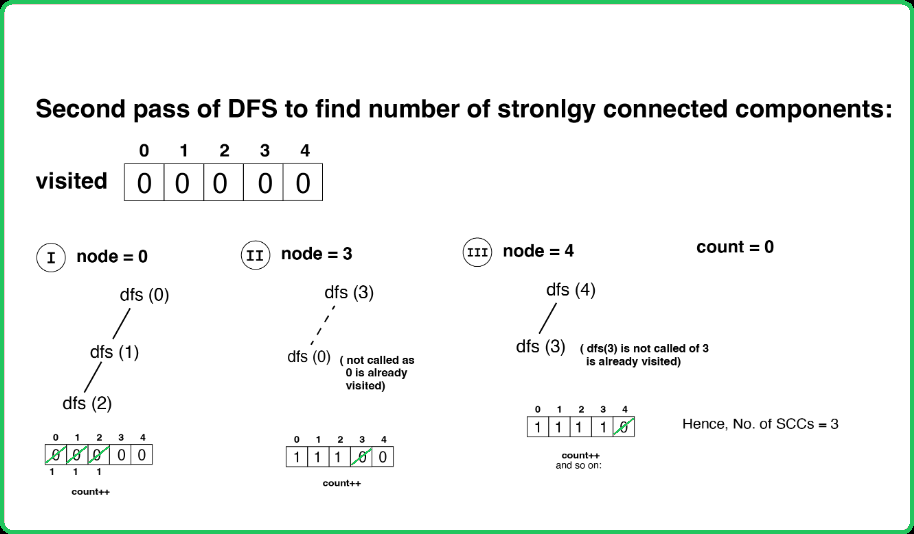
- Perform the DFS and count the number of different DFS calls to get the number of SCC: Start DFS traversal on the reversed graph from the node which is on the top of the stack and continue until the stack becomes empty. For each DFS call, the counter representing the number of SCCs can be incremented by 1.
Approach:
- Create a visited array to keep track of visited nodes and a stack to store nodes based on their finishing times during DFS traversal.
- Perform a DFS on the original graph to determine the finishing times of nodes. Each node is pushed onto the stack after all its descendants are processed.
- Reverse the edges of the original graph to create a transposed graph. Perform DFS on the transposed graph, starting from the nodes in the order defined by the stack (based on their finishing times from the first DFS).
- Count the number of DFS trees formed in this step, which corresponds to the number of strongly connected components.
- The count of DFS trees from the second pass is the number of strongly connected components in the original graph.
Dry Run:
Solution:
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126
#include <bits/stdc++.h>
using namespace std;
class Solution {
private:
/* Function to perform DFS for storing the
nodes in stack based on their finishing time */
void dfs(int node, vector<int> &vis, vector<int> adj[],
stack<int> &st) {
// Mark the node as visited
vis[node] = 1;
// Traverse all its neighbors
for (auto it : adj[node]) {
if (!vis[it]) {
// Recursively perform DFS is not visited already
dfs(it, vis, adj, st);
}
}
// Push the node in stack
st.push(node);
}
/* Helper function to perform DFS for finding
number of Strongly connected components */
void helperDFS(int node, vector<int> &vis,
vector<int> adjT[]) {
// Mark the node as visited
vis[node] = 1;
// Traverse all its neighbors
for (auto it : adjT[node]) {
if (!vis[it]) {
// Recursively perform DFS if not already visited
helperDFS(it, vis, adjT);
}
}
}
public:
/* Funtion call to find the number of
strongly connected components */
int kosaraju(int V, vector<int> adj[]) {
// Visited array
vector<int> vis(V, 0);
// Stack data structure
stack<int> st;
/* Perform initial DFS to store the nodes
in stack based on their finishing time */
for (int i = 0; i < V; i++) {
if (!vis[i]) {
dfs(i, vis, adj, st);
}
}
// To store the revered graph
vector<int> adjT[V];
/* Reverse all the edges of original
graph to the reversed graph */
for (int i = 0; i < V; i++) {
// Mark the node as unvisited
vis[i] = 0;
// Add the reversed edge
for (auto it : adj[i]) {
adjT[it].push_back(i);
}
}
/* To store the count of strongly
connected components */
int count = 0;
/* Start DFS call from every unvisited
node based on their finishing time */
while (!st.empty()) {
// Get the node
int node = st.top();
st.pop();
// If not visited already
if (!vis[node]) {
count += 1;
helperDFS(node, vis, adjT);
}
}
// Return the result
return count;
}
};
int main() {
int n = 5;
int edges[5][2] = {
{1, 0}, {0, 2},
{2, 1}, {0, 3},
{3, 4}
};
// Creating the adjacency list
vector<int> adj[n];
for (int i = 0; i < n; i++) {
adj[edges[i][0]].push_back(edges[i][1]);
}
// Creating an instance of Solution class
Solution obj;
/* Funtion call to find the number of
strongly connected components */
int ans = obj.kosaraju(n, adj);
cout << "The number of strongly connected components is: " << ans << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115
import java.util.*;
class Solution {
/* Function to perform DFS for storing the
nodes in stack based on their finishing time */
private void dfs(int node, int[] vis,
ArrayList<ArrayList<Integer>> adj,
Stack<Integer> st) {
// Mark the node as visited
vis[node] = 1;
// Traverse all its neighbors
for (int it : adj.get(node)) {
if (vis[it] == 0) {
// Recursively perform DFS if not visited already
dfs(it, vis, adj, st);
}
}
// Push the node in stack
st.push(node);
}
/* Helper function to perform DFS for finding
number of Strongly connected components */
private void helperDFS(int node, int[] vis,
ArrayList<ArrayList<Integer>> adjT) {
// Mark the node as visited
vis[node] = 1;
// Traverse all its neighbors
for (int it : adjT.get(node)) {
if (vis[it] == 0) {
// Recursively perform DFS if not already visited
helperDFS(it, vis, adjT);
}
}
}
/* Funtion call to find the number of
strongly connected components */
public int kosaraju(int V, ArrayList<ArrayList<Integer>> adj) {
// Visited array
int[] vis = new int[V];
// Stack data structure
Stack<Integer> st = new Stack<>();
/* Perform initial DFS to store the nodes
in stack based on their finishing time */
for (int i = 0; i < V; i++) {
if (vis[i] == 0) {
dfs(i, vis, adj, st);
}
}
// To store the reversed graph
ArrayList<ArrayList<Integer>> adjT = new ArrayList<>();
for (int i = 0; i < V; i++) {
adjT.add(new ArrayList<>());
}
/* Reverse all the edges of original
graph to the reversed graph */
for (int i = 0; i < V; i++) {
// Mark the node as unvisited
vis[i] = 0;
// Add the reversed edge
for (int it : adj.get(i)) {
adjT.get(it).add(i);
}
}
/* To store the count of strongly
connected components */
int count = 0;
/* Start DFS call from every unvisited
node based on their finishing time */
while (!st.isEmpty()) {
// Get the node
int node = st.pop();
// If not visited already
if (vis[node] == 0) {
count += 1;
helperDFS(node, vis, adjT);
}
}
// Return the result
return count;
}
public static void main(String[] args) {
int V = 5;
ArrayList<ArrayList<Integer>> adj = new ArrayList<>();
for (int i = 0; i < V; i++) {
adj.add(new ArrayList<>());
}
adj.get(0).add(2);
adj.get(0).add(3);
adj.get(1).add(0);
adj.get(2).add(1);
adj.get(3).add(4);
Solution sol = new Solution();
int count = sol.kosaraju(V, adj);
System.out.println("Number of strongly connected components: " + count);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081
class Solution:
def dfs(self, node, vis, adj, st):
# Mark the node as visited
vis[node] = 1
# Traverse all its neighbors
for it in adj[node]:
if not vis[it]:
# Recursively perform DFS if not visited already
self.dfs(it, vis, adj, st)
# Push the node in stack
st.append(node)
def helperDFS(self, node, vis, adjT):
# Mark the node as visited
vis[node] = 1
# Traverse all its neighbors
for it in adjT[node]:
if not vis[it]:
# Recursively perform DFS if not already visited
self.helperDFS(it, vis, adjT)
def kosaraju(self, V, adj):
# Visited array
vis = [0] * V
# Stack data structure
st = []
''' Perform initial DFS to store the nodes
in stack based on their finishing time '''
for i in range(V):
if not vis[i]:
self.dfs(i, vis, adj, st)
# To store the reversed graph
adjT = [[] for _ in range(V)]
''' Reverse all the edges of original
graph to the reversed graph '''
for i in range(V):
# Mark the node as unvisited
vis[i] = 0
# Add the reversed edge
for it in adj[i]:
adjT[it].append(i)
''' To store the count of strongly
connected components '''
count = 0
''' Start DFS call from every unvisited
node based on their finishing time '''
while st:
# Get the node
node = st.pop()
# If not visited already
if not vis[node]:
count += 1
self.helperDFS(node, vis, adjT)
# Return the result
return count
# Main function
if __name__ == "__main__":
V = 5
adj = [[] for _ in range(V)]
adj[0].extend([2, 3])
adj[1].append(0)
adj[2].append(1)
adj[3].append(4)
sol = Solution()
count = sol.kosaraju(V, adj)
print("Number of strongly connected components:", count)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103
class Solution {
/* Function to perform DFS for storing the nodes
in stack based on their finishing time */
dfs(node, vis, adj, st) {
// Mark the node as visited
vis[node] = 1;
// Traverse all its neighbors
adj[node].forEach(it => {
if (!vis[it]) {
// Recursively perform DFS if not visited already
this.dfs(it, vis, adj, st);
}
});
// Push the node in stack
st.push(node);
}
/* Helper function to perform DFS for finding
number of Strongly connected components */
helperDFS(node, vis, adjT) {
// Mark the node as visited
vis[node] = 1;
// Traverse all its neighbors
adjT[node].forEach(it => {
if (!vis[it]) {
// Recursively perform DFS if not already visited
this.helperDFS(it, vis, adjT);
}
});
}
/* Function call to find the number of
strongly connected components */
kosaraju(V, adj) {
// Visited array
let vis = new Array(V).fill(0);
// Stack data structure
let st = [];
/* Perform initial DFS to store the nodes
in stack based on their finishing time */
for (let i = 0; i < V; i++) {
if (!vis[i]) {
this.dfs(i, vis, adj, st);
}
}
// To store the revered graph
let adjT = new Array(V).fill(null).map(() => []);
/* Reverse all the edges of original
graph to the reversed graph */
for (let i = 0; i < V; i++) {
// Mark the node as unvisited
vis[i] = 0;
// Add the reversed edge
adj[i].forEach(it => {
adjT[it].push(i);
});
}
/* To store the count of strongly
connected components */
let count = 0;
/* Start DFS call from every unvisited
node based on their finishing time */
while (st.length > 0) {
// Get the node
let node = st.pop();
// If not visited already
if (!vis[node]) {
count += 1;
this.helperDFS(node, vis, adjT);
}
}
// Return the result
return count;
}
}
// Main function
(function() {
const V = 5;
let adj = new Array(V).fill(null).map(() => []);
adj[0].push(2);
adj[0].push(3);
adj[1].push(0);
adj[2].push(1);
adj[3].push(4);
let sol = new Solution();
let count = sol.kosaraju(V, adj);
console.log("Number of strongly connected components:", count);
})();
Complexity Analysis:
Time Complexity: O(V+E) (where E represent the number of edges)
Two DFS traversals are made each taking an O(V+E) time. Reversing all the edges in the graph takes O(E) time.
Space Complexity: O(V+E)
Storing the transposed graph takes O(V+E) space and the space due to the stack and visited array will be O(V) each.