Kadane's Algorithm
Arrays
FAQs(Medium)
Medium
- This problem, often referred to as the Maximum Subarray Problem, forms the basis for many real-world applications in the field of Financial Technology
- One key application is in the analysis of stock prices
- Given the changes in a stock's price over a sequence of time (which can be positive or negative), the maximum subarray problem can be used to determine the most profitable time to buy and sell for maximum profit
- The subarray with the largest sum essentially represents the period with the most significant growth
- The Kadane's algorithm, often used to solve this problem, is widely used in such financial analysis systems, reinforcing how theoretical computer science problems have direct, practical implications
Given an integer array nums, find the subarray with the largest sum and return the sum of the elements present in that subarray.
A subarray is a contiguous non-empty sequence of elements within an array.
Examples:
Input: nums = [2, 3, 5, -2, 7, -4]
Output: 15
Explanation: The subarray from index 0 to index 4 has the largest sum = 15
Input: nums = [-2, -3, -7, -2, -10, -4]
Output: -2
Explanation: The element on index 0 or index 3 make up the largest sum when taken as a subarray
Input: nums = [-1, 2, 3, -1, 2, -6, 5]
Constraints
- 1 <= nums.length <= 105
- -104 <= nums[i] <= 104
Hints
- "Maintain two variables: currentMax: Tracks the maximum sum ending at the current index. globalMax: Stores the maximum sum seen so far."
- If adding the current element decreases the sum, start a new subarray from the current element. This happens when the previous sum becomes negative.
Company Tags
Activision Blizzard
Broadcom
Teladoc Health
Roche
Zomato
Pinterest
Optum
Epic Systems
Twilio
Rockstar Games
Siemens Healthineers
Red Hat
McKinsey & Company
Oracle
Cloudflare
Mastercard
Salesforce
Seagate Technology
Qualcomm
Flipkart
Bain & Company
PwC
Electronic Arts
Swiggy
Philips Healthcare
Google
Microsoft
Amazon
Meta
Apple
Netflix
Adobe
Editorial
Intuition
The idea is to find out all the subarrays of the given array and while finding out the subarray calculate the sum of all the elements of that particular subarray. Finally, find out the maximum sum among them and that will be the result.
Approach
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152
#include<bits/stdc++.h>
using namespace std;
class Solution {
public:
//Function to find maximum sum of subarrays
int maxSubArray(vector<int>& nums) {
/* Initialize maximum sum with
the smallest possible integer*/
int maxi = INT_MIN;
// Iterate over each starting index of subarrays
for (int i = 0; i < nums.size(); i++) {
/* Iterate over each ending index
of subarrays starting from i*/
for (int j = i; j < nums.size(); j++) {
// Variable to store the sum of the current subarray
int sum = 0;
// Calculate the sum of subarray nums[i...j]
for (int k = i; k <= j; k++) {
sum += nums[k];
}
/* Update maxi with the maximum of its current
value and the sum of the current subarray*/
maxi = max(maxi, sum);
}
}
// Return the maximum subarray sum found
return maxi;
}
};
int main() {
vector<int> arr = { -2, 1, -3, 4, -1, 2, 1, -5, 4};
//create an instance of Solution class
Solution sol;
int maxSum = sol.maxSubArray(arr);
//Print the max subarray sum
cout << "The maximum subarray sum is: " << maxSum << endl;
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849
import java.util.*;
class Solution {
// Function to find maximum sum of subarrays
public int maxSubArray(int[] nums) {
/* Initialize maximum sum with
the smallest possible integer*/
int maxi = Integer.MIN_VALUE;
// Iterate over each starting index of subarrays
for (int i = 0; i < nums.length; i++) {
/* Iterate over each ending index
of subarrays starting from i*/
for (int j = i; j < nums.length; j++) {
/* Variable to store the sum
of the current subarray*/
int sum = 0;
// Calculate the sum of subarray nums[i...j]
for (int k = i; k <= j; k++) {
sum += nums[k];
}
/* Update maxi with the maximum of its current
value and the sum of the current subarray*/
maxi = Math.max(maxi, sum);
}
}
// Return the maximum subarray sum found
return maxi;
}
public static void main(String[] args) {
int[] arr = { -2, 1, -3, 4, -1, 2, 1, -5, 4};
// Create an instance of Solution class
Solution sol = new Solution();
int maxSum = sol.maxSubArray(arr);
// Print the max subarray sum
System.out.println("The maximum subarray sum is: " + maxSum);
}
}
12345678910111213141516171819202122232425262728293031323334353637383940414243
from typing import List
class Solution:
# Function to find maximum sum of subarrays
def maxSubArray(self, nums: list[int]) -> int:
""" Initialize maximum sum with
the smallest possible integer"""
maxi = float('-inf')
# Iterate over each starting index of subarrays
for i in range(len(nums)):
""" Iterate over each ending index
of subarrays starting from i"""
for j in range(i, len(nums)):
""" Variable to store the sum
of the current subarray"""
sum = 0
# Calculate the sum of subarray nums[i...j]
for k in range(i, j + 1):
sum += nums[k]
""" Update maxi with the maximum of itscurrent
value and the sum of the current subarray"""
maxi = max(maxi, sum)
# Return the maximum subarray sum found
return maxi
# Test
arr = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
#create an isinstance of Solution class
sol = Solution()
maxSum = sol.maxSubArray(arr)
#Print the max sum of subarrays
print("The maximum subarray sum is:", maxSum)
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051
class Solution {
// Function to find maximum sum of subarrays
maxSubArray(nums) {
/* Initialize maximum sum with
the smallest possible integer*/
let maxi = -Infinity;
// Iterate over each starting index of subarrays
for (let i = 0; i < nums.length; i++) {
/* Iterate over each ending index
of subarrays starting from i*/
for (let j = i; j < nums.length; j++) {
/* Variable to store the sum
of the current subarray*/
let sum = 0;
// Calculate the sum of subarray nums[i...j]
for (let k = i; k <= j; k++) {
sum += nums[k];
}
/* Update maxi with the maximum of its current
value and the sum of the current subarray*/
maxi = Math.max(maxi, sum);
}
}
// Return the maximum subarray sum found
return maxi;
}
}
// Main function to test the Solution class
function main() {
let arr = [-2, 1, -3, 4, -1, 2, 1, -5, 4];
// Create an instance of Solution class
let sol = new Solution();
let maxSum = sol.maxSubArray(arr);
// Print the max subarray sum
console.log("The maximum subarray sum is: " + maxSum);
}
main();
Complexity Analysis
Time Complexity: O(N3), where N is the size of the array. Using three nested loops, each running approximately N times. Space Complexity: O(1) no extra space used.Intuition
The better approach is to avoid triple looping structure mentioned previously that calculates the sum of each subarray. On observation we understand that to get the sum of the current subarray we just need to add the current element to the sum of the previous subarray, hence there is no need of third loop to do that.
Approach
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// Function to find maximum sum of subarrays
int maxSubArray(vector<int>& nums) {
/* Initialize maximum sum with
the smallest possible integer*/
int maxi = INT_MIN;
// Iterate over each starting index of subarrays
for (int i = 0; i < nums.size(); i++) {
/* Variable to store the sum
of the current subarray*/
int sum = 0;
/* Iterate over each ending index
of subarrays starting from i*/
for (int j = i; j < nums.size(); j++) {
/* Add the current element nums[j] to
the sum i.e. sum of nums[i...j-1]*/
sum += nums[j];
/* Update maxi with the maximum of its current
value and the sum of the current subarray*/
maxi = max(maxi, sum);
}
}
// Return the maximum subarray sum found
return maxi;
}
};
int main() {
vector<int> arr = { -2, 1, -3, 4, -1, 2, 1, -5, 4 };
// Create an instance of Solution class
Solution sol;
int maxSum = sol.maxSubArray(arr);
// Print the max subarray sum
cout << "The maximum subarray sum is: " << maxSum << endl;
return 0;
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748
import java.util.*;
class Solution {
// Function to find maximum sum of subarrays
public int maxSubArray(int[] nums) {
/* Initialize maximum sum with
the smallest possible integer*/
int maxi = Integer.MIN_VALUE;
// Iterate over each starting index of subarrays
for (int i = 0; i < nums.length; i++) {
/* Variable to store the sum
of the current subarray*/
int sum = 0;
/* Iterate over each ending index
of subarrays starting from i*/
for (int j = i; j < nums.length; j++) {
/* Add the current element nums[j] to
the sum i.e. sum of nums[i...j-1]*/
sum += nums[j];
/* Update maxi with the maximum of its current
value and the sum of the current subarray*/
maxi = Math.max(maxi, sum);
}
}
// Return the maximum subarray sum found
return maxi;
}
public static void main(String[] args) {
int[] arr = { -2, 1, -3, 4, -1, 2, 1, -5, 4 };
// Create an instance of Solution class
Solution sol = new Solution();
int maxSum = sol.maxSubArray(arr);
// Print the max subarray sum
System.out.println("The maximum subarray sum is: " + maxSum);
}
}
1234567891011121314151617181920212223242526272829303132333435363738394041424344
from typing import List
class Solution:
# Function to find maximum sum of subarrays
def maxSubArray(self, nums: List[int]) -> int:
""" Initialize maximum sum with
the smallest possible integer"""
maxi = float('-inf')
# Iterate over each starting index of subarrays
for i in range(len(nums)):
""" Variable to store the sum
of the current subarray"""
sum = 0
""" Iterate over each ending index
of subarrays starting from i"""
for j in range(i, len(nums)):
""" Add the current element nums[j] to
the sum i.e. sum of nums[i...j-1]"""
sum += nums[j]
""" Update maxi with the maximum of its current
value and the sum of the current subarray"""
maxi = max(maxi, sum)
# Return the maximum subarray sum found
return maxi
# Main function to test the Solution class
if __name__ == "__main__":
arr = [-2, 1, -3, 4, -1, 2, 1, -5, 4]
# Create an instance of Solution class
sol = Solution()
maxSum = sol.maxSubArray(arr)
# Print the max subarray sum
print(f"The maximum subarray sum is: {maxSum}")
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849
class Solution {
// Function to find maximum sum of subarrays
maxSubArray(nums) {
/* Initialize maximum sum with
the smallest possible integer*/
let maxi = -Infinity;
// Iterate over each starting index of subarrays
for (let i = 0; i < nums.length; i++) {
/* Variable to store the sum
of the current subarray*/
let sum = 0;
/* Iterate over each ending index
of subarrays starting from i*/
for (let j = i; j < nums.length; j++) {
/* Add the current element nums[j] to
the sum i.e. sum of nums[i...j-1]*/
sum += nums[j];
/* Update maxi with the maximum of its current
value and the sum of the current subarray*/
maxi = Math.max(maxi, sum);
}
}
// Return the maximum subarray sum found
return maxi;
}
}
function main() {
let arr = [ -2, 1, -3, 4, -1, 2, 1, -5, 4 ];
// Create an instance of Solution class
let sol = new Solution();
let maxSum = sol.maxSubArray(arr);
// Print the max subarray sum
console.log("The maximum subarray sum is: " + maxSum);
}
// Execute the main function
main();
Complexity Analysis
Time Complexity:O(N2), for using two nested loops, each running approximately N times, here N is the size of the array. Space Complexity: O(1) for not using any extra space.Intuition
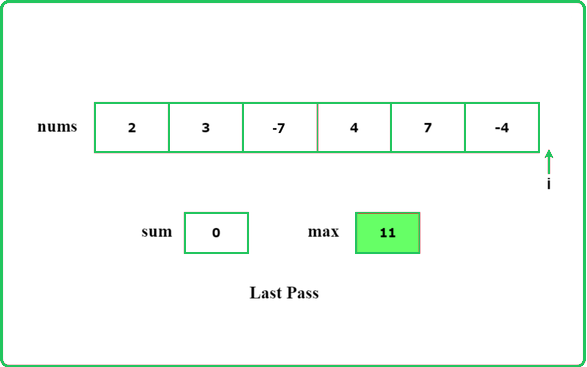
The intuition of the algorithm is to not consider the subarray as a part of the answer if its sum is less than 0. A subarray with a sum less than 0 will always reduce the answer and so this type of subarray cannot be a part of the subarray with maximum sum.
Approach
Dry Run
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950
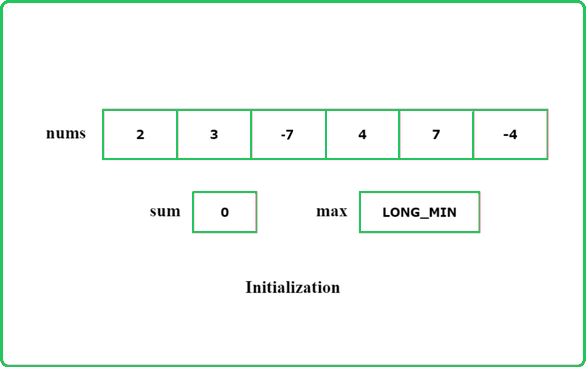
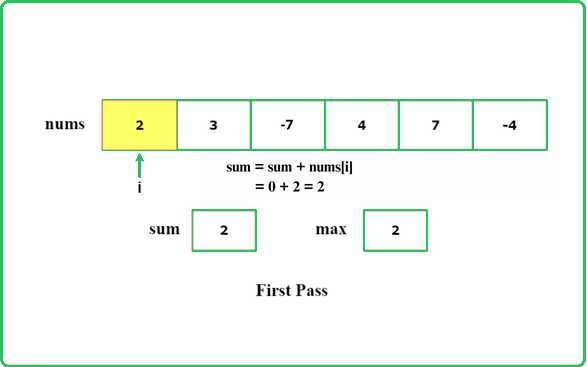
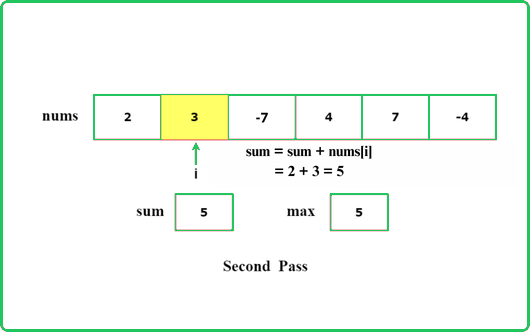
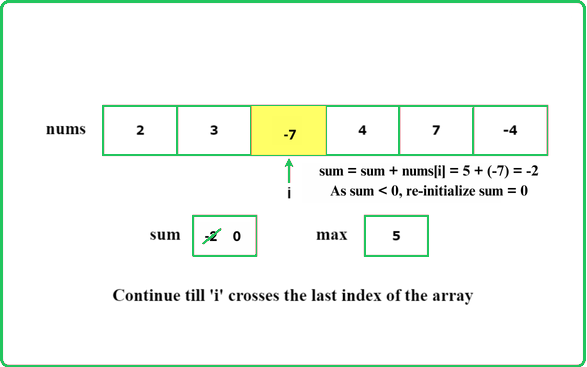
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// Function to find maximum sum of subarrays
int maxSubArray(vector<int>& nums) {
// maximum sum
long long maxi = LLONG_MIN;
// current sum of subarray
long long sum = 0;
// Iterate through the array
for (int i = 0; i < nums.size(); i++) {
// Add current element to the sum
sum += nums[i];
// Update maxi if current sum is greater
if (sum > maxi) {
maxi = sum;
}
// Reset sum to 0 if it becomes negative
if (sum < 0) {
sum = 0;
}
}
// Return the maximum subarray sum found
return maxi;
}
};
int main() {
vector<int> arr = { -2, 1, -3, 4, -1, 2, 1, -5, 4 };
// Create an instance of Solution class
Solution sol;
int maxSum = sol.maxSubArray(arr);
// Print the max subarray sum
cout << "The maximum subarray sum is: " << maxSum << endl;
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546
import java.util.*;
class Solution {
// Function to find maximum sum of subarrays
public int maxSubArray(int[] nums) {
// maximum sum
long maxi = Long.MIN_VALUE;
//current sum of subarray
long sum = 0;
// Iterate through the array
for (int i = 0; i < nums.length; i++) {
// Add current element to the sum
sum += nums[i];
// Update maxi if current sum is greater
if (sum > maxi) {
maxi = sum;
}
// Reset sum to 0 if it becomes negative
if (sum < 0) {
sum = 0;
}
}
// Return the maximum subarray sum found
return (int) maxi;
}
public static void main(String[] args) {
int[] arr = { -2, 1, -3, 4, -1, 2, 1, -5, 4 };
// Create an instance of Solution class
Solution sol = new Solution();
int maxSum = sol.maxSubArray(arr);
// Print the max subarray sum
System.out.println("The maximum subarray sum is: " + maxSum);
}
}
12345678910111213141516171819202122232425262728293031323334353637383940
from typing import List
class Solution:
# Function to find maximum sum of subarrays
def maxSubArray(self, nums: List[int]) -> int:
# maximum sum
maxi = float('-inf')
# current sum of subarray
sum = 0
# Iterate through the array
for i in range(len(nums)):
# Add current element to the sum
sum += nums[i]
# Update maxi if current sum is greater
if sum > maxi:
maxi = sum
# Reset sum to 0 if it becomes negative
if sum < 0:
sum = 0
# Return the maximum subarray sum found
return maxi
if __name__ == "__main__":
arr = [ -2, 1, -3, 4, -1, 2, 1, -5, 4 ]
# Create an instance of Solution class
sol = Solution()
maxSum = sol.maxSubArray(arr)
# Print the max subarray sum
print(f"The maximum subarray sum is: {maxSum}")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647
class Solution {
// Function to find maximum sum of subarrays
maxSubArray(nums) {
// maximum sum
let maxi = -Infinity;
// current sum of subarray
let sum = 0;
// Iterate through the array
for (let i = 0; i < nums.length; i++) {
// Add current element to the sum
sum += nums[i];
// Update maxi if current sum is greater
if (sum > maxi) {
maxi = sum;
}
// Reset sum to 0 if it becomes negative
if (sum < 0) {
sum = 0;
}
}
// Return the maximum subarray sum found
return maxi;
}
}
function main() {
let arr = [ -2, 1, -3, 4, -1, 2, 1, -5, 4 ];
// Create an instance of Solution class
let sol = new Solution();
let maxSum = sol.maxSubArray(arr);
// Print the max subarray sum
console.log("The maximum subarray sum is: " + maxSum);
}
// Execute the main function
main();
Complexity Analysis
Time Complexity: O(N) for single traversal, here N is the size of the array. Space Complexity: O(1), for not using any extra space.Follow up question
Can you print the subarray that has the max sum ?
Intuition
The idea is to store the starting index and the ending index of the subarray. Thus its easily possible to get the subarray with maximum sum afterward without actually storing the subarray elements. On careful observation we can notice that the subarray always starts at the particular index where the sum variable is equal to 0, and at the ending index, the sum always crosses the previous maximum sum. Using this observation print the subarray with maximum sum.
Approach
Note that submitting this code will throw an error.
Solution:
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
// Function to find maximum sum of subarrays and print the subarray having maximum sum
int maxSubArray(vector<int>& nums) {
// maximum sum
long long maxi = LLONG_MIN;
// current sum of subarray
long long sum = 0;
// starting index of current subarray
int start = 0;
// indices of the maximum sum subarray
int ansStart = -1, ansEnd = -1;
// Iterate through the array
for (int i = 0; i < nums.size(); i++) {
// update starting index if sum is reset
if (sum == 0) {
start = i;
}
// add current element to the sum
sum += nums[i];
/* Update maxi and subarray indice
s if current sum is greater*/
if (sum > maxi) {
maxi = sum;
ansStart = start;
ansEnd = i;
}
// Reset sum to 0 if it becomes negative
if (sum < 0) {
sum = 0;
}
}
// Printing the subarray
cout << "The subarray is: [";
for (int i = ansStart; i <= ansEnd; i++) {
cout << nums[i] << " ";
}
cout << "]" << endl;
// Return the maximum subarray sum found
return maxi;
}
};
int main() {
vector<int> arr = { -2, 1, -3, 4, -1, 2, 1, -5, 4 };
// Create an instance of Solution class
Solution sol;
int maxSum = sol.maxSubArray(arr);
// Print the max subarray sum
cout << "The maximum subarray sum is: " << maxSum << endl;
return 0;
}
12345678910111213141516171819202122232425262728293031323334353637383940414243444546474849505152535455565758596061626364656667
import java.util.*;
class Solution {
// Function to find maximum sum of subarrays and print the subarray having maximum sum
public int maxSubArray(int[] nums) {
// maximum sum
long maxi = Long.MIN_VALUE;
// current sum of subarray
long sum = 0;
// starting index of current subarray
int start = 0;
// indices of the maximum sum subarray
int ansStart = -1, ansEnd = -1;
// Iterate through the array
for (int i = 0; i < nums.length; i++) {
// update starting index if sum is reset
if (sum == 0) {
start = i;
}
// add current element to the sum
sum += nums[i];
/* Update maxi and subarray indices
if current sum is greater */
if (sum > maxi) {
maxi = sum;
ansStart = start;
ansEnd = i;
}
// Reset sum to 0 if it becomes negative
if (sum < 0) {
sum = 0;
}
}
// Printing the subarray
System.out.print("The subarray is: [");
for (int i = ansStart; i <= ansEnd; i++) {
System.out.print(nums[i] + " ");
}
System.out.println("]");
// Return the maximum subarray sum found
return (int) maxi;
}
public static void main(String[] args) {
int[] arr = { -2, 1, -3, 4, -1, 2, 1, -5, 4 };
// Create an instance of Solution class
Solution sol = new Solution();
int maxSum = sol.maxSubArray(arr);
// Print the max subarray sum
System.out.println("The maximum subarray sum is: " + maxSum);
}
}
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960
from typing import List
class Solution:
# Function to find maximum sum of subarrays and print the subarray having maximum sum
def maxSubArray(self, nums: List[int]) -> int:
# maximum sum
maxi = float('-inf')
# current sum of subarray
sum = 0
# starting index of current subarray
start = 0
# indices of the maximum sum subarray
ansStart = -1
ansEnd = -1
# Iterate through the array
for i in range(len(nums)):
# update starting index if sum is reset
if sum == 0:
start = i
# add current element to the sum
sum += nums[i]
""" Update maxi and subarray indices
if current sum is greater """
if sum > maxi:
maxi = sum
ansStart = start
ansEnd = i
# Reset sum to 0 if it becomes negative
if sum < 0:
sum = 0
# Printing the subarray
print("The subarray is: [", end="")
for i in range(ansStart, ansEnd + 1):
print(nums[i], end=" ")
print("]")
# Return the maximum subarray sum found
return maxi
if __name__ == "__main__":
arr = [ -2, 1, -3, 4, -1, 2, 1, -5, 4 ]
# Create an instance of Solution class
sol = Solution()
maxSum = sol.maxSubArray(arr)
# Print the max subarray sum
print(f"The maximum subarray sum is: {maxSum}")
1234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768
class Solution {
// Function to find maximum sum of subarrays and print the subarray having maximum sum
maxSubArray(nums) {
// maximum sum
let maxi = -Infinity;
// current sum of subarray
let sum = 0;
// starting index of current subarray
let start = 0;
// indices of the maximum sum subarray
let ansStart = -1, ansEnd = -1;
// Iterate through the array
for (let i = 0; i < nums.length; i++) {
// update starting index if sum is reset
if (sum === 0) {
start = i;
}
// add current element to the sum
sum += nums[i];
/* Update maxi and subarray indices
if current sum is greater */
if (sum > maxi) {
maxi = sum;
ansStart = start;
ansEnd = i;
}
// Reset sum to 0 if it becomes negative
if (sum < 0) {
sum = 0;
}
}
// Printing the subarray
process.stdout.write("The subarray is: [");
for (let i = ansStart; i <= ansEnd; i++) {
process.stdout.write(nums[i] + " ");
}
console.log("]");
// Return the maximum subarray sum found
return maxi;
}
}
function main() {
let arr = [ -2, 1, -3, 4, -1, 2, 1, -5, 4 ];
// Create an instance of Solution class
let sol = new Solution();
let maxSum = sol.maxSubArray(arr);
// Print the max subarray sum
console.log("The maximum subarray sum is: " + maxSum);
}
// Execute the main function
main();
Complexity Analysis
Time Complexity: O(N), for using a single loop running N times, where N is the size of the array. Space Complexity: O(1), for not using any extra space.Frequently Occurring Doubts
Q: Why use Kadane’s algorithm instead of nested loops?
A: Kadane’s algorithm runs in O(n) time, making it much more efficient than the O(n^2) or O(n^3) time of nested loop approaches. It processes each element only once.
Interview Followup Questions
Q: How would you generalize this to find the largest subarray sum for 2D arrays (matrices)?
A: For a 2D matrix: Use Kadane’s algorithm on each possible submatrix. Iterate over row pairs, calculating the sum of elements in each submatrix and applying Kadane’s algorithm to find the largest subarray sum.
Q: How would you modify Kadane’s algorithm to return the actual subarray?
A: Track the start and end indices of the maximum subarray: When starting a new subarray (currentMax = nums[i]), record the start index. Update the end index when globalMax is updated.
Notes
Code
✅ Testcase
Input: {'nums': '[2, 3, 5, -2, 7, -4]'}
Expected:
15
15
Actual: -
Time: -
sec
Status: Waiting
Input: {'nums': '[-2, -3, -7, -2, -10, -4]'}
Expected:
-2
-2
Actual: -
Time: -
sec
Status: Waiting
Input: {'nums': '[-1, 2, 3, -1, 2, -6, 5]'}
Expected:
6
6
Actual: -
Time: -
sec
Status: Waiting