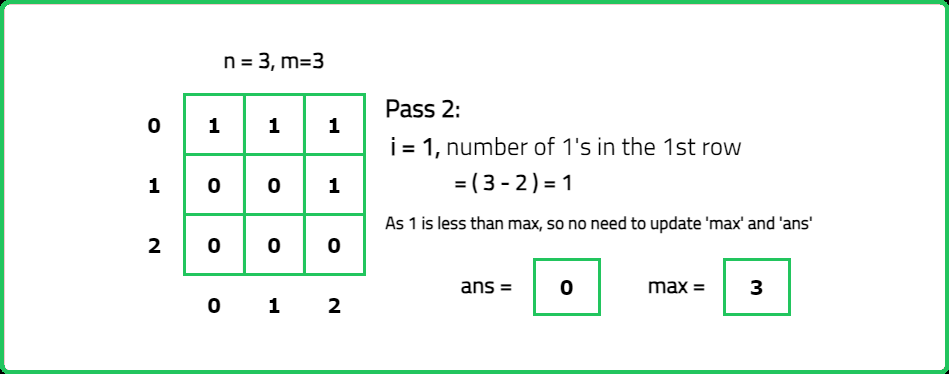
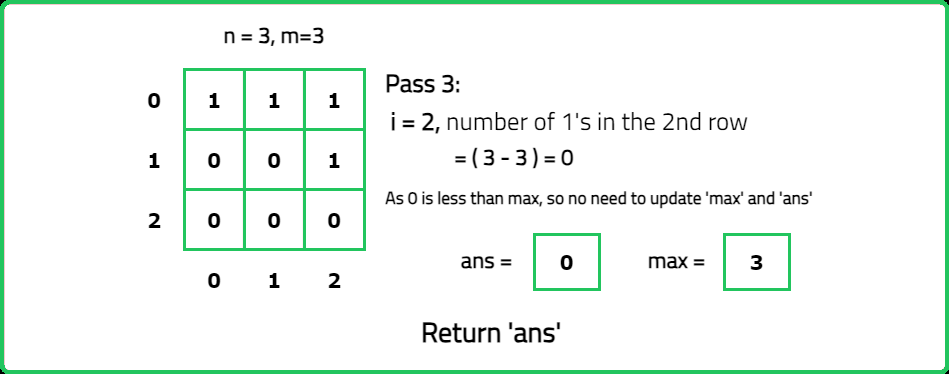
Find row with maximum 1's

Binary Search 2D Arrays Hard

One real-world application of this problem can be found in Image Processing
Notably, in the case of binary images, which consists solely of 1s (indicating white pixels) and 0s (indicating black pixels)
By finding the row with the most white pixels (1s), certain characteristics of the image can be determined, such as the location of an object within the image
This concept is at the heart of many computer vision tasks that form the basis for features like facial recognition in apps like Facebook and Snapchat

Given a non-empty grid mat consisting of only 0s and 1s, where all the rows are sorted in ascending order, find the index of the row with the maximum number of ones.

Examples:

Input : mat = [ [1, 1, 1], [0, 0, 1], [0, 0, 0] ]

Output: 0

Explanation: The row with the maximum number of ones is 0 (0 - indexed).

Input: mat = [ [0, 0], [0, 0] ]

Output: -1

Explanation: The matrix does not contain any 1. So, -1 is the answer.

Input : mat = [ [0, 0, 1], [0, 1, 1], [0, 1, 1] ]

Constraints

n == mat.length
m == mat[i].length
1 <= n, m <= 100
mat[i][j] is either 0 or 1.

Hints

"Since rows are sorted, the first 1 in a row determines the count of 1s. If a row contains n columns and the first 1 appears at index j, then the count of 1s in that row is n−j."
For each row, use binary search to find the index of the first 1. Keep track of the row with the maximum number of 1s as you iterate through the grid.

Company Tags

Alibaba JPMorgan Chase PwC Ernst & Young Roblox Zoho Philips Healthcare Salesforce Robinhood Uber GE Healthcare Visa ARM Cloudflare Wayfair Square Riot Games Epic Games DoorDash Optum Intel Epic Systems McKinsey & Company Docker Bloomberg Google Microsoft Amazon Meta Apple Netflix Adobe

Intuition:

The extremely naive approach is to traverse the matrix as usual using nested loops and for every single row count the number of 1’s. Finally, return the row with the maximum no. of 1’s. If multiple rows contain the maximum no. of 1’s, return the row with the minimum index.

Approach:

First, declare two variables: cnt_max initialized with 0 to store the maximum number of 1’s found and index initialized with -1 to store the row number.
Next, start traversing the matrix using nested loops to get each cell of the matrix. For each row count the number of 1's.
After that, compare it with cnt_max and if the current number of 1’s is greater, update cnt_max with the current no. of 1’s and ‘index’ with the current row index.
Finally, return the variable ‘index’. It will store the index of the row with the maximum no. of 1’s. And otherwise, it will store -1 if there is no 1's in the matrix at all.

#include <bits/stdc++.h>
using namespace std;

class Solution {
public:
    /* Function to find the row 
    with the maximum number of 1's*/
    int rowWithMax1s(vector<vector<int>>& mat) {
        int n = mat.size();
        int m = mat[0].size();
        
        /* Variable to store the 
        maximum count of 1's found*/
        int cnt_max = 0; 
        
        /* Variable to store the index
        of the row with max 1's*/
        int index = -1;  

        // Traverse the matrix row by row
        for (int i = 0; i < n; i++) {
            
            /* Counter for 1's 
            in the current row*/
            int cnt_ones = 0; 

            /* Count the number of 
            1's in the current row*/
            for (int j = 0; j < m; j++) {
                cnt_ones += mat[i][j];
            }

            /* Update cnt_max and index if current
            row has more 1's than previously found*/
            if (cnt_ones > cnt_max) {
                cnt_max = cnt_ones;
                index = i;
            }
        }

        /* Return the index of the row 
        with the maximum number of 1's*/
        return index;
    }
};

int main() {
    vector<vector<int>> matrix = {{1, 1, 1}, {0, 0, 1}, {0, 0, 0}};
    
    // Create an instance of the Solution class
    Solution sol; 
    
    // Print the answer
    cout << "The row with maximum number of 1's is: " <<
            sol.rowWithMax1s(matrix) << '\n';

    return 0;
}
import java.util.*;

class Solution {
    /* Function to find the row 
    with the maximum number of 1's*/
    public int rowWithMax1s(int[][] mat) {
        int n = mat.length;
        int m = mat[0].length;
        
        /* Variable to store the 
        maximum count of 1's found*/
        int cnt_max = 0; 
        
        /* Variable to store the index
        of the row with max 1's*/
        int index = -1;  

        // Traverse the matrix row by row
        for (int i = 0; i < n; i++) {
            
            /* Counter for 1's 
            in the current row*/
            int cnt_ones = 0; 

            /* Count the number of 
            1's in the current row*/
            for (int j = 0; j < m; j++) {
                cnt_ones += mat[i][j];
            }

            /* Update cnt_max and index if current
            row has more 1's than previously found*/
            if (cnt_ones > cnt_max) {
                cnt_max = cnt_ones;
                index = i;
            }
        }

        /* Return the index of the row 
        with the maximum number of 1's*/
        return index;
    }

    public static void main(String[] args) {
        int[][] matrix = {{1, 1, 1}, {0, 0, 1}, {0, 0, 0}};

        // Create an instance of the Solution class
        Solution sol = new Solution();
        
        // Print the answer
        System.out.println("The row with maximum number of 1's is: " + 
                sol.rowWithMax1s(matrix));
    }
}
class Solution:
    """ Function to find the row 
    with the maximum number of 1's"""
    def rowWithMax1s(self, mat):
        n = len(mat)
        m = len(mat[0])
        """ Variable to store the 
        maximum count of 1's found"""
        cnt_max = 0 
        
        """ Variable to store the index
        of the row with max 1's"""
        index = -1  

        # Traverse the matrix row by row
        for i in range(n):
            
            """ Counter for 1's 
            in the current row"""
            cnt_ones = 0 

            """ Count the number of 
            1's in the current row"""
            for j in range(m):
                cnt_ones += mat[i][j]

            """ Update cnt_max and index if current
            row has more 1's than previously found"""
            if cnt_ones > cnt_max:
                cnt_max = cnt_ones
                index = i

        """ Return the index of the row 
        with the maximum number of 1's"""
        return index

if __name__ == "__main__":
    matrix = [[1, 1, 1], [0, 0, 1], [0, 0, 0]]
    
    # Create an instance of the Solution class
    sol = Solution()
    
    # Print the answer
    print("The row with maximum number of 1's is:", sol.rowWithMax1s(matrix))
class Solution {
    /* Function to find the row 
    with the maximum number of 1's*/
    rowWithMax1s(mat) {
        let n = mat.length;
        let m = mat[0].length;
        /* Variable to store the 
        maximum count of 1's found*/
        let cnt_max = 0; 
        
        /* Variable to store the index
        of the row with max 1's*/
        let index = -1;  

        // Traverse the matrix row by row
        for (let i = 0; i < n; i++) {
            
            /* Counter for 1's 
            in the current row*/
            let cnt_ones = 0; 

            /* Count the number of 
            1's in the current row*/
            for (let j = 0; j < m; j++) {
                cnt_ones += mat[i][j];
            }

            /* Update cnt_max and index if current
            row has more 1's than previously found*/
            if (cnt_ones > cnt_max) {
                cnt_max = cnt_ones;
                index = i;
            }
        }

        /* Return the index of the row 
        with the maximum number of 1's*/
        return index;
    }
}

const matrix = [[1, 1, 1], [0, 0, 1], [0, 0, 0]];

//Create an instance of Solution class
const sol = new Solution();

// Print the answer
console.log("The row with maximum number of 1's is: " + sol.rowWithMax1s(matrix));

Complexity Analysis:

Time Complexity: O(N X M), where N is the number of rows in the matrix, M is the number of columns in each row. As, nested loops are being used to traverse the matrix.

Space Complexity: As no additional space is used, so the Space Complexity is O(1).

Intuition:

The idea here is to use Binary Search to optimize the brute-force solution where linear search was being used. Since, each row of the given matrix is sorted, Binary Search can be applied on each row to find the Lower Bound of 1, as lower bound gives the very first index such that element on that index is either equal to 1 or greater than 1. So, total number of 1's in each row can be calculated as: lower bound of 1 subtracted from total number of columns. Do the same of each row and return the index of row having maximum 1's or in case of multiple rows having maximum 1's, return the smallest index. Finally, if there is no 1 in the matrix return -1.

Approach:

Working of rowWithMax1s(matrix):

First, declare two variables: cnt_max initialized with 0 to store the maximum number of 1’s found and index initialized with -1 to store the row number.
Next, start traversing the rows of the matrix using a for loop. For each row call the lowerBound() function to get the first occurrence of 1(0 based indexing). Calculate the total number of 1's in each row by subtraction the first occurrence of 1 from total columns.
After that, compare it with cnt_max and if the current number of 1’s is greater, update cnt_max with the current no. of 1’s and ‘index’ with the current row index.
Finally, return the variable ‘index’. It will store the index of the row with the maximum no. of 1’s. And otherwise, it will store -1 if there is no 1's in the matrix at all.

Working of lowerBound(arr, n, x):

Start with initializing low = 0 and high = n - 1, where n is the total columns of the matrix. Initialize 'ans' to n, which serves as the default answer assuming no element in the array is greater than or equal to x.
Initialize a while loop to perform binary search until low exceeds high. Calculate the 'mid' index as (low + high) / 2.
If arr[mid] greater than or equal to x. This means it's a potential candidate for being the lower bound (first element that is not less than x). Update ans to mid, indicating that we found a potential lower bound. Then adjust high to mid - 1 to search for a potentially smaller lower bound on the left side of mid. Otherwise, move low to mid + 1 to search for the lower bound on the right side of mid.
When the while loop terminates, return 'ans'.

#include <bits/stdc++.h>
using namespace std;

class Solution {
private:
    //Helper function to find the lower bound of 1.
    int lowerBound(vector<int> arr, int n, int x) {
    int low = 0, high = n - 1;
    int ans = n;

    while (low <= high) {
        int mid = (low + high) / 2;
        
        /* If element at mid is greater than or equal 
        to x then it counld be a possible answer.*/
        if (arr[mid] >= x) {
            ans = mid;
            
            //Look for smaller index on the left
            high = mid - 1;
        }
        else {
            low = mid + 1; 
        }
    }
    //Return the answer
    return ans;
}
public:
    /* Function to find the row 
    with the maximum number of 1's*/
    int rowWithMax1s(vector<vector<int>>& mat) {
        int n = mat.size();
        int m = mat[0].size();
        
        /* Variable to store the 
        maximum count of 1's found*/
        int cnt_max = 0; 
        
        /* Variable to store the index
        of the row with max 1's*/
        int index = -1;  

        //Traverse each row of the matrix
        for (int i = 0; i < n; i++) {
            // Get the number of 1's
            int cnt_ones = m - lowerBound(mat[i], m, 1);
            
            /*If the current count is greater than 
            maximum, store the index of current row
            and update the maximum count.*/
            if (cnt_ones > cnt_max) {
                cnt_max = cnt_ones;
                index = i;
            }
        }

        /* Return the index of the row 
        with the maximum number of 1's*/
        return index;
    }
};

int main() {
    vector<vector<int>> matrix = {{1, 1, 1}, {0, 0, 1}, {0, 0, 0}};
    
    // Create an instance of the Solution class
    Solution sol; 
    
    // Print the answer
    cout << "The row with maximum number of 1's is: " <<
            sol.rowWithMax1s(matrix) << '\n';

    return 0;
}
import java.util.*;

class Solution {
    // Helper function to find the lower bound of 1.
    private int lowerBound(int[] arr, int n, int x) {
        int low = 0, high = n - 1;
        int ans = n;

        while (low <= high) {
            int mid = (low + high) / 2;
            
            /* If element at mid is greater than or equal 
            to x then it counld be a possible answer.*/
            if (arr[mid] >= x) {
                ans = mid;
                
                // Look for smaller index on the left
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        // Return the answer
        return ans;
    }

    /* Function to find the row 
    with the maximum number of 1's*/
    public int rowWithMax1s(int[][] mat) {
        int n = mat.length;
        int m = mat[0].length;
        
        /* Variable to store the 
        maximum count of 1's found*/
        int cnt_max = 0; 
        
        /* Variable to store the index
        of the row with max 1's*/
        int index = -1;  

        // Traverse each row of the matrix
        for (int i = 0; i < n; i++) {
            // Get the number of 1's
            int cnt_ones = m - lowerBound(mat[i], m, 1);
            
            /* If the current count is greater than 
            maximum, store the index of current row
            and update the maximum count.*/
            if (cnt_ones > cnt_max) {
                cnt_max = cnt_ones;
                index = i;
            }
        }

        /* Return the index of the row 
        with the maximum number of 1's*/
        return index;
    }

    public static void main(String[] args) {
        int[][] matrix = {{1, 1, 1}, {0, 0, 1}, {0, 0, 0}};
        
        // Create an instance of the Solution class
        Solution sol = new Solution(); 
        
        // Print the answer
        System.out.println("The row with maximum number of 1's is: " +
                sol.rowWithMax1s(matrix));
    }
}
class Solution:
    # Helper function to find the lower bound of 1.
    def lowerBound(self,arr, n, x):
        low, high = 0, n - 1
        ans = n

        while low <= high:
            mid = (low + high) // 2
                
            """If element at mid is greater than or equal 
            to x then it could be a possible answer."""
            if arr[mid] >= x:
                ans = mid
                    
                # Look for smaller index on the left
                high = mid - 1
            else:
                low = mid + 1
            
        # Return the answer
        return ans
        
    """ Function to find the row 
    with the maximum number of 1's"""
    def rowWithMax1s(self, mat):
        n = len(mat)
        m = len(mat[0])
        
        """ Variable to store the 
        maximum count of 1's found"""
        cnt_max = 0 
        
        """ Variable to store the index
        of the row with max 1's"""
        index = -1  

        # Traverse each row of the matrix
        for i in range(n):
            # Get the number of 1's
            cnt_ones = m - self.lowerBound(mat[i], m, 1)
            
            """ If the current count is greater than 
            maximum, store the index of current row
            and update the maximum count."""
            if cnt_ones > cnt_max:
                cnt_max = cnt_ones
                index = i
        
        """ Return the index of the row 
        with the maximum number of 1's"""
        return index

if __name__ == "__main__":
    matrix = [[1, 1, 1], [0, 0, 1], [0, 0, 0]]
    
    # Create an instance of the Solution class
    sol = Solution()
    
    # Print the answer
    print("The row with maximum number of 1's is:", sol.rowWithMax1s(matrix))
class Solution {
    // Helper function to find the lower bound of 1.
    lowerBound(arr, n, x) {
        let low = 0, high = n - 1;
        let ans = n;

        while (low <= high) {
            let mid = Math.floor((low + high) / 2);
                
            /* If element at mid is greater than or equal 
               to x then it could be a possible answer. */
            if (arr[mid] >= x) {
                ans = mid;
                
                // Look for smaller index on the left
                high = mid - 1;
            } else {
                low = mid + 1;
            }
        }
        // Return the answer
        return ans;
    }
    
    /* Function to find the row 
       with the maximum number of 1's */
    rowWithMax1s(mat) {
        let n = mat.length;
        let m = mat[0].length;
        
        /* Variable to store the 
           maximum count of 1's found */
        let cnt_max = 0; 
        
        /* Variable to store the index
           of the row with max 1's */
        let index = -1;  

        // Traverse each row of the matrix
        for (let i = 0; i < n; i++) {
            // Get the number of 1's
            let cnt_ones = m - this.lowerBound(mat[i], m, 1);
            
            /* If the current count is greater than 
               maximum, store the index of current row
               and update the maximum count. */
            if (cnt_ones > cnt_max) {
                cnt_max = cnt_ones;
                index = i;
            }
        }

        /* Return the index of the row 
           with the maximum number of 1's */
        return index;
    }
}

const matrix = [[1, 1, 1], [0, 0, 1], [0, 0, 0]];

// Create an instance of Solution class
const sol = new Solution();

// Print the answer
console.log("The row with maximum number of 1's is: " + sol.rowWithMax1s(matrix));

Complexity Analysis:

Time Complexity:O(N * logM), where N is the number of rows in the matrix, M is the number of columns in each row. As, each row is being traversed once and then binary search is being applied for M columns of every row.

Space Complexity: As no additional space is used, so the Space Complexity is O(1).

Code

Problem List

Find row with maximum 1's

Examples:

Constraints

Hints

Company Tags

Editorial

Intuition:

Approach:

Complexity Analysis:

Intuition:

Approach:

Complexity Analysis:

Frequently Occurring Doubts

Interview Followup Questions

Notes

Code