Dijkstra's algorithm

Dijkstra's Algorithm:

Dijkstra's Algorithm is used in connected graphs (undirected as well as directed) whenever it is required to find out the shortest distance from the source node to every other node.

Conditions for Dijkstra's Algorithm to work?

The graph must not have any non-negative edge weights.

Algorithm:

Set the distance to the starting node as 0 and to all other nodes as infinity. Add all nodes to an unvisited set. Begin with the starting node.
Perform Edge Relaxation i.e., for each unvisited neighbor of the current node, calculate the tentative distance from the start node. If this tentative distance is less than the known distance, update it.
Mark the current node as visited once all its neighbors have been evaluated. It won't be checked again. Choose the unvisited node with the smallest tentative distance as the new current node.
Repeat steps 2-3 untill all the nodes are visited. Once all nodes are visited, the shortest path to all the nodes is now known.

Implementation: Using Min-Heap

To implement the Dijkstra's Algorithm, a minimum heap data structure (Priority Queue) can be used. The priority queue will store the pair {dist, node} storing the tentative distance required to reach the node from the source node. If this distance is found to be smaller than the known distance, we update the distance to reach node and push to newly found pair of {dist, node} in the priority queue.

Significance of using a Min-Heap data structure:

Storing the pair {dist, node} in min-heap ensures that out of all the pairs, the node with the minimum distance (from source node) is taken into consideration first. This helps the algorithm to explore the shortest path first improving efficiency.

Approach:

Use a priority queue to process nodes by their shortest known distance.
Initialize an array to store shortest distances, with the source node set to 0 and all others to infinity.
Add the source node to the priority queue with a distance of 0.
Extract the node with the smallest distance from the queue and perfom edge relaxation (update the distances to its neighbors if a shorter path is found). Add the updated neighbors back to the queue.
The distance array contains the shortest distances from the source to all node.

Dry Run:

#include <bits/stdc++.h>
using namespace std;

/* Define P as a shorthand 
for the pair<int, int> type */
#define P pair<int,int>

class Solution {
public:
    /* Function to find the shortest distance of all 
    the vertices from the source vertex S. */
    vector <int> dijkstra(int V, vector<vector<int>> adj[], 
                          int S) {
                                
        // Priority queue 
        priority_queue <P, vector<P>, greater<P>> pq;
        
        // Distance array
        vector<int> dist(V, 1e9);
        
        // Distance of source node from itself is 0
        dist[S] = 0;
        
        // Add the source node to the priority queue
        pq.push({0, S});
        
        // Until the priority queue is empty
        while(!pq.empty()) {
            
            // Get the tentative distance
            int dis = pq.top().first;
            
            // Get the node
            int node = pq.top().second;
            pq.pop();
            
            // Traverse all its neighbors
            for(auto it : adj[node]) {
                
                int adjNode = it[0]; // node
                int edgeWt = it[1]; // edge weight
                
                /* If the tentative distance to 
                reach adjacent node is smaller 
                than the known distance */
                if(dis + edgeWt < dist[adjNode]) {
                    
                    // Update the known distance
                    dist[adjNode] = dis + edgeWt;
                    
                    // Push the new pair in priority queue
                    pq.push({dist[adjNode], adjNode});
                }
            }
        }
        
        // Return the result
        return dist;
    }
};

int main() {
    
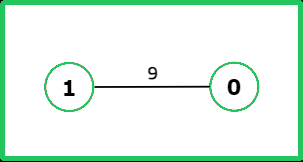
    int V = 2, S = 0;
    vector<vector<int>> adj[V] = {
        {{1, 9}}, 
        {{0, 9}}
    };
    
    /* Creating an instance of 
    Solution class */
    Solution sol; 
    
    /* Function call to find the shortest distance 
    of each node from the source node */
    vector<int> ans = sol.dijkstra(V, adj, S);
    
    // Output
    cout << "The shortest distance of nodes from the source node is: ";
    for(int i=0; i < V; i++) {
        cout << ans[i] << " ";
    }
    
    return 0;
}
import java.util.*;

class Solution {
    /* Function to find the shortest distance of all 
    the vertices from the source vertex S. */
    public int[] dijkstra(int V, 
        ArrayList<ArrayList<ArrayList<Integer>>> adj, int S) {
        
        // Priority queue
        PriorityQueue<int[]> pq = new PriorityQueue<>(
            Comparator.comparingInt(a -> a[0])
        );
        
        // Distance array
        int[] dist = new int[V];
        Arrays.fill(dist, (int) 1e9);
        
        // Distance of source node from itself is 0
        dist[S] = 0;
        
        // Add the source node to the priority queue
        pq.add(new int[]{0, S});
        
        // Until the priority queue is empty
        while (!pq.isEmpty()) {
            
            // Get the tentative distance
            int dis = pq.peek()[0];
            
            // Get the node
            int node = pq.peek()[1];
            pq.poll();
            
            // Traverse all its neighbors
            for (ArrayList<Integer> it : adj.get(node)) {
                
                int adjNode = it.get(0); // node
                int edgeWt = it.get(1); // edge weight
                
                /* If the tentative distance to 
                reach adjacent node is smaller 
                than the known distance */
                if (dis + edgeWt < dist[adjNode]) {
                    
                    // Update the known distance
                    dist[adjNode] = dis + edgeWt;
                    
                    // Push the new pair in priority queue
                    pq.add(new int[]{dist[adjNode], adjNode});
                }
            }
        }
        
        // Return the result
        return dist;
    }
}

class Main {
    public static void main(String[] args) {
        
        int V = 2, S = 0;
        
        // Create adjacency list
        ArrayList<ArrayList<ArrayList<Integer>>> adj = new ArrayList<>();
        ArrayList<ArrayList<Integer>> node0 = new ArrayList<>();
        node0.add(new ArrayList<>(Arrays.asList(1, 9)));
        adj.add(node0);
        
        ArrayList<ArrayList<Integer>> node1 = new ArrayList<>();
        node1.add(new ArrayList<>(Arrays.asList(0, 9)));
        adj.add(node1);
        
        /* Creating an instance of 
        Solution class */
        Solution sol = new Solution();
        
        /* Function call to find the shortest distance 
        of each node from the source node */
        int[] ans = sol.dijkstra(V, adj, S);
        
        // Output
        System.out.print("The shortest distance of nodes from the source node is: ");
        for (int i = 0; i < V; i++) {
            System.out.print(ans[i] + " ");
        }
        System.out.println();
    }
}
import heapq

class Solution:
    # Function to find the shortest distance of all
    # the vertices from the source vertex S.
    def dijkstra(self, V, adj, S):
        
        # Priority queue
        pq = []
        
        # Distance array
        dist = [int(1e9)] * V
        
        # Distance of source node from itself is 0
        dist[S] = 0
        
        # Add the source node to the priority queue
        heapq.heappush(pq, (0, S))
        
        # Until the priority queue is empty
        while pq:
            
            # Get the tentative distance
            dis, node = heapq.heappop(pq)
            
            # Traverse all its neighbors
            for adjNode, edgeWt in adj[node]:
                
                # If the tentative distance to reach adjacent node
                # is smaller than the known distance
                if dis + edgeWt < dist[adjNode]:
                    
                    # Update the known distance
                    dist[adjNode] = dis + edgeWt
                    
                    # Push the new pair in priority queue
                    heapq.heappush(pq, (dist[adjNode], adjNode))
        
        # Return the result
        return dist


# Main method
if __name__ == "__main__":
    V, S = 2, 0
    
    # Create adjacency list
    adj = [
        [(1, 9)], 
        [(0, 9)]
    ]
    
    # Creating an instance of Solution class
    sol = Solution()
    
    # Function call to find the shortest distance
    # of each node from the source node
    ans = sol.dijkstra(V, adj, S)
    
    # Output
    print("The shortest distance of nodes from the source node is:", end=" ")
    for i in ans:
        print(i, end=" ")
    print()
// Minimum Priority Queue Implementation
class MinPriorityQueue {
    constructor() {
        this.heap = [];
    }

    // Insert a new element in the priority queue
    push(element) {
        this.heap.push(element);
        this.bubbleUp(this.heap.length - 1);
    }

    /* Remove and return the element with the 
    highest priority (smallest element) */
    pop() {
        if (this.heap.length === 1) return this.heap.pop();

        const min = this.heap[0];
        this.heap[0] = this.heap.pop();
        this.bubbleDown(0);

        return min;
    }

    // Get the element with the highest priority without removing it
    peek() {
        return this.heap[0];
    }

    // Return true if the priority queue is empty */
    isEmpty() {
        return this.heap.length === 0;
    }

    // Restore heap order after adding a new element
    bubbleUp(index) {
        const element = this.heap[index];
        while (index > 0) {
            const parentIndex = Math.floor((index - 1) / 2);
            const parent = this.heap[parentIndex];
            if (element[0] >= parent[0]) break;
            this.heap[index] = parent;
            index = parentIndex;
        }
        this.heap[index] = element;
    }

    // Restore heap order after removing an element
    bubbleDown(index) {
        const length = this.heap.length;
        const element = this.heap[index];

        while (true) {
            let leftIndex = 2 * index + 1;
            let rightIndex = 2 * index + 2;
            let swapIndex = null;

            if (leftIndex < length) {
                if (this.heap[leftIndex][0] < element[0]) {
                    swapIndex = leftIndex;
                }
            }

            if (rightIndex < length) {
                if (
                    (swapIndex === null && this.heap[rightIndex][0] < element[0]) ||
                    (swapIndex !== null && this.heap[rightIndex][0] < this.heap[swapIndex][0])
                ) {
                    swapIndex = rightIndex;
                }
            }

            if (swapIndex === null) break;
            this.heap[index] = this.heap[swapIndex];
            index = swapIndex;
        }
        this.heap[index] = element;
    }
}

class Solution {
    /* Function to find the shortest distance of all 
    the vertices from the source vertex S. */
    dijkstra(V, adj, S) {
        // Custom min-priority queue
        let pq = new MinPriorityQueue();
        
        // Distance array
        let dist = new Array(V).fill(1e9);
        
        // Distance of source node from itself is 0
        dist[S] = 0;
        
        // Add the source node to the priority queue
        pq.push([0, S]);
        
        // Until the priority queue is empty
        while (!pq.isEmpty()) {
            // Get the tentative distance
            let [dis, node] = pq.pop();
            
            // Traverse all its neighbors
            for (let it of adj[node]) {
                let adjNode = it[0]; // node
                let edgeWt = it[1]; // edge weight
                
                /* If the tentative distance to 
                reach adjacent node is smaller 
                than the known distance */
                if (dis + edgeWt < dist[adjNode]) {
                    // Update the known distance
                    dist[adjNode] = dis + edgeWt;
                    
                    // Push the new pair in priority queue
                    pq.push([dist[adjNode], adjNode]);
                }
            }
        }
        
        // Return the result
        return dist;
    }
}

let V = 2, S = 0;
let adj = [
    [[1, 9]], 
    [[0, 9]]
];

/* Creating an instance of 
Solution class */
let sol = new Solution();

/* Function call to find the shortest distance 
of each node from the source node */
let ans = sol.dijkstra(V, adj, S);

// Output
console.log("The shortest distance of nodes from the source node is: ");
for (let i = 0; i < V; i++) {
    console.log(ans[i] + " ");
}

Complexity Analysis:

Time Complexity: O((V+E)*logV) (where V and E represent the number of nodes and edges of the graph)

Each node is processed once in the priority queue and deletion and insertion operation takes O(logV) time making it overall O(V*logV) in the worst case.
For each vertex, all its edges are relaxed. This operation involves updating the priority queue, which takes O(logV) making it overall O(E*logV) for E edges in the worst case.

Space Complexity: O(V)

The priority queue will store distances to all nodes in worst case leading to O(V) space.
The distance array takes O(V) space.